Lasso polymer chains, which have the simplest structure among multi-cyclic polymer chains, possess both the properties of cyclic polymers and those of linear polymers. In this study, we designed three kinds of lasso polymer systems and used them to closely investigate the changes in their properties depending on the polymer molecular structure. The lasso polymer chains under shear flow exhibited different structural, dynamic, and rheological properties despite having the same molecular weight. In addition, the lasso polymer chains exhibited different chain tumbling and rotation mechanisms at high shear flow strength.

멀티 고리형 고분자 체인 중 가장 간단한 구조를 가지는 올가미형 고분자 체인은 고리형 고분자의 특성과 선형 고분자의 특성을 동시에 가지고 있다. 본 연구에서는 이러한 특성을 지닌 세 가지 종류의 올가미형 고분자 시스템을 고안하였고 이를 이용하여 고분자 분자 구조에 따른 특성 변화를 면밀히 조사하였다. 전단 유동하 올가미형 고분자 체인들은 같은 분자량을 가짐에도 불구하고 각기 다른 구조적, 동역학적, 유변학적 특성을 보여주었다. 또한, 올가미형 고분자 체인들은 높은 전단 세기에서 각기 다른 체인 텀블링 및 회전 메커니즘을 보여주었다.

Lasso polymer chains, which have the simplest structure among multi-cyclic polymer chains, possess both the properties of cyclic polymers and those of linear cyclic polymers. We designed three kinds of lasso polymer systems and used them to closely investigate the changes in their properties depending on the polymer molecular structure. In particular, the lasso polymer chains exhibited different chain tumbling and rotation mechanisms at high shear flow strength as shown below.

Keywords: multicyclic polymer, lasso polymer, Brownian dynamics, shear flow, computer simulation.

2021학년도 경기대학교 학술연구비(신진연구과제) 지원에 의하여 수행되었음.

저자들은 이해상충이 없음을 선언합니다.

현대의 편리한 생활을 영위하는데 있어 필수불가결한 고분자(polymer) 제품들은 다양한 연속적인 흐름 공정(continuous flow processing)을 거쳐 제조된다. 이러한 고분자 가공 과정(polymer processing)에 있어 고분자의 분자 구조(molecular architecture)는 고분자의 물리적, 동역학적, 유변학적 특성들에 큰 영향을 미친다. 따라서, 고분자 과학자들은 고분자의 분자 구조와 그에 따른 특성들의 관계를 찾기 위해 끊임없이 노력하고 있다. 하지만, 고분자는 모노머의 종류 및 길이에 따라 무수히 많은 분자 구조를 가질 수 있다. 이러한 이유 때문에 우리는 고분자의 구조-특성 관계(structure-property relationship)를 찾아내는데 많은 어려움을 겪고 있는 실정이다.^1,2
최근 수십 년간 더욱 발전한 고분자 합성 기술 덕분에 우리는 기존 고분자와는 다른 특성을 지닌 새로운 고분자를 합성할 수 있게 되었다.^1-5 예를 들어, 선형 고분자(linear polymer)의 양쪽 체인 끝을 이어 만들어낸 고리형 고분자(ring polymer)는 기존 고분자와는 다른 특성을 보여준다. 고리형 고분자는 같은 분자량을 가진 선형 고분자보다 빠른 확산(faster diffusion), 빠른 이완 시간(faster relaxation time), 낮은 점도(lower viscosity), 높은 유리 전이 온도(higher glass transition temperature) 등을 보여준다.^6-23 특히, 고리형 고분자는 자유 체인 끝(free chain end)이 없는 독특한 폐쇄 루프 구조(intrinsic closed-loop structure)를 갖기 때문에 기존 고분자 동역학 이론 및 모델을 이용하여 고리형 고분자의 거동을 설명할 수 없다.²⁴ 이에 따라 지난 수십 년간 고리형 고분자의 특성을 설명하기 위해 많은 이론과 모델들이 제시되었으며 최근 실험기술의 발전과 함께 괄목할 만한 성과를 거두고 있다.^25-38 현재 이러한 고리형 고분자 이론과 모델을 개선하기 위해 고분자 과학자들은 고리형 체인 간 관통 효과(ring threading effect)에 집중하고 있다.^20,21
현재는 순수한 고리형 고분자(monocyclic polymer)에 대한 이해를 바탕으로 좀 더 복잡한 형태의 멀티 고리형 고분자(multicyclic polymer)들이 합성되고 있다.^4,39-48 다수의 고리(ring)와 다수의 선형 곁가지(linear side branch)로 이루어진 멀티 고리형 고분자는 고리형 고분자와 선형 고분자의 특징을 동시에 지니고 있기 때문에 기존 고리형 고분자(monocyclic polymer)보다 더욱 다양한 물리화학적 성질과 독특한 동역학적 거동을 보여주고 있다.^39-48 특히, 생물학적 시스템에서 멀티 고리형 고분자 구조를 지닌 바이오 분자들이 많이 발견되기 때문에 멀티 고리형 고분자 체인의 활용영역은 새로운 소재 개발에서부터 바이오 분야까지 광범위하게 펼쳐져 있다.^46-50 멀티 고리형 고분자는 고리의 개수, 선형 곁가지의 개수, 분기점(junction point)의 배치에 따라 크게 ‘fused’, ‘spiro’, ‘bridged’의 세 가지 타입으로 분류할 수 있다.⁴ 예를 들어, ‘fused’ 타입의 대표적인 고분자는 세타 모양의 고분자(theta-shaped polymer)이고 ‘spiro’ 타입의 대표적인 고분자는 8모양의 고분자(8-shaped polymer)이며, bridged 타입의 대표적인 고분자는 수갑 모양의 고분자(manacle polymer)이다.
멀티 고리형 고분자 중 선형 고분자와 고리형 고분자의 구조적인 특성을 동시에 지니고 있는 고분자는 올가미형 고분자(lasso polymer)이다. 참고로 올챙이형 고분자(tadpole polymer)라고 불리기도 한다. 올가미형 고분자는 하나의 고리 부분과 하나의 선형 곁가지로 이루어져 있기 때문에 자유로운 체인 끝(free chain end)을 가질 뿐만 아니라 독특한 폐쇄 루프 구조(intrinsic closed-loop structure)를 가진다. 이러한 독특한 분자 구조 때문에 올가미형 고분자는 약물 전달 물질, 나노 와이어, 나노 튜브, 윤활제 등과 같은 다양한 소재에 쓰이기도 하며 바이오 분야에 매우 유용하게 활용되어질 것으로 예상된다. 예를 들어, 항생제로 쓰이고 있는 lasso peptides는 올가미형 고분자와 매우 유사한 구조를 가진다. 따라서, 올가미형 고분자에 관한 연구는 향후 이러한 생체 단백질 분자의 작동 메커니즘을 이해하는데 있어 매우 핵심적인 역할을 할 것이라 기대된다.
현재 다양한 멀티 고리형 고분자들이 합성되고 있지만, 이러한 고분자들에 대한 물리적, 동역학적, 유변학적 특성에 관한 연구는 전무한 편이다. 따라서, 본 연구에서는 거친 입자 브라운 동역학 전산모사(coarse-grained Brownian dynamics simulation)를 이용하여 멀티 고리형 고분자 중 가장 간단한 구조를 가지고 있는 올가미형 고분자의 특성을 조사하였다. 본 연구에서는 간접적인 용매 효과를 반영한 고립된 비드-로드 브라운 동역학 전산모사(isolated bead-rod Brownian dynamics simulation)를 이용하였기 때문에 고리형 고분자의 관통 효과(ring threading effect)를 배제할 수 있었고 이에 따라 순수한 올가미 형태 고분자 체인의 유체역학적 구조 변화와 유변학적 거동을 조사할 수 있었다. 일반적으로 같은 분자량을 가진 고분자 체인 시스템들은 비슷한 구조적, 동역학적, 유변학적 특성을 보이는데 반하여 같은 분자량을 지닌 올가미 형태의 고분자 체인 시스템들은 분자 구조에 따라 각기 다른 구조적, 물리적, 동역학적, 유변학적 특성을 보여주었다.

전산모사방법. 본 연구에서는 올가미형 고분자 체인의 유체역학적 구조 변화와 유변학적 거동을 조사하기 위해 광범위한 거친 입자 브라운 동역학 전산모사(coarse-grained Brownian dynamics simulation)를 실행하였으며, 올가미형 고분자 체인들을 효율적으로 묘사하기 위해 간접적인 용매 효과를 반영한 고립된 비드-로드 체인 분자(bead-rod chain molecules)를 사용하였다. 특히, 이상적인 올가미형 고분자 체인의 유체역학적 구조와 유변학적 거동을 살펴보기 위해 유체역학적 상호작용(hydrodynamic interactions, HI) 및 배제 체적 효과(excluded volume effect, EV)가 고려되지 않은 자유 배수 용액 시스템(free-draining solution system)을 사용하였다. 자유 배수 용액 시스템에서 고분자 체인의 거친 브라운 동역학 전산모사는 고분자 용용체(polymeric melts)나 고농축 용액(highly concentrated solutions)에서의 고분자 체인의 거동을 잘 예측한다고 알려져 있다.⁵¹
거친 입자의 브라운 동역학 전산모사에서 자유롭게 연결된 각각의 비드(freely jointed bead)에는 세 가지 외부 힘(external forces)이 작용한다고 가정한다. 이로부터 우리는 시간에 따른 비드의 위치를 계산해 낼 수 있다. 시간에 따른 비드의 거동은 위치 벡터(position vector)를 이용해서 묘사하거나 연결 벡터(connector vector)를 이용하여 묘사할 수 있다. 본 연구에서는 위치 벡터를 이용하여 시간에 따른 비드의 거동을 묘사하였고 아래와 같은 확률 미분 방정식(stochastic differential equation, SDE) 형태의 일반적인 확산 방정식(diffusion equation)으로 시간에 따른 비드의 거동을 기술할 수 있었다.⁵¹



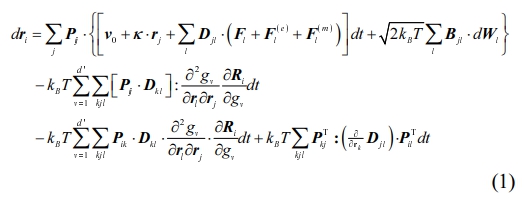
여기서, r_i는 비드 i의 위치 벡터(position vector)를 나타내고 있으며, P_ij는 동적 투영 텐서(dynamical projection tensor)를 나타낸다. F_i는 임의의 비드에 작용하는 내부 힘(internal forces)을 의미하고, F_i^(e)
는 임의의 비드에 작용하는 외부 힘(external forces)을 나타내며, F_i^(m)는 임의의 비드에 작용하는 메트릭 힘(metric force)을 나타낸다. D_ij는 모빌리티 텐서(mobility tensor)이고 B_ij는 모빌리티 텐서의 분해 텐서(decomposed tensor of the mobility tensor)이며, 아래와 같은 관계를 가진다.



W_i는 비드 i에 대한 시간에 의존하는 랜덤 변수를 나타낸다. k_B는 볼츠만 상수(Boltzmann constant)이고 g_v는 제약 조건(constraint)이다. k는 속도 기울기 텐서로서 아래와 같이 정의된다.



여기서 γ̀는 전단율(shear rate)을 나타낸다. 자유롭게 연결된 비드-로드(freely-jointed bead-rod) 체인을 이용한 올가미형 고분자의 거친 입자 브라운 동역학 전산모사에서 위치 벡터에 관한 확률 미분 방정식은 Liu의 반복 방법(iterative technique)을 통해 수치적으로 적분된다.⁵²
고분자 체인 시스템. 전단 유동(shear flow) 하 올가미형 고분자의 분자 구조가 고분자의 유체역학적 거동 및 형태(hydrodynamics behavior and structure)에 미치는 영향을 체계적으로 조사 및 분석하기 위해 같은 분자량 또는 비드 수(same molecular weight or number of beads)를 가진 세 가지 고분자 체인 시스템을 고안하였다.
Figure 1에서 보듯이, 세 가지 올가미형 고분자를 구성하는 전체 비드 수는 66개이며 각 시스템에 따라 고리형 백본(ring backbone)과 선형 곁가지(linear side branch) 부분에 속한 비드 수가 달라진다. 먼저, 50개의 비드로 구성된 고리형 백본에 16개의 비드로 구성된 선형 곁가지가 결합된 고분자 체인을 ‘cyclic_1tail’ 고분자 체인이라고 표기하였고(Figure 1(a)), 50개의 비드로 구성된 고리형 백본 양쪽에 8개의 비드로 구성된 두 개의 선형 곁가지가 결합된 고분자 체인을 ‘cyclic_2tails’ 고분자 체인이라고 표기하였다(Figure 1(b)). 마지막으로 42개의 비드로 구성된 고리형 백본을 따라 일정 간격으로 8개의 비드로 구성된 세 개의 선형 곁가지가 결합된 고분자 체인을 ‘cyclic_3tails’ 고분자 체인이라고 표기하였다(Figure 1(c)). 전단 유동 하에서 선형 폴리에틸렌(linear polyethylene)의 경우 하나의 비드(bead)는 대략 6개의 CH₂ 원자에 해당한다고 알려져 있다.⁵³ 따라서, 현재 비드-로드 모델(bead-rod model)을 이용한 올가미형 고분자 체인의 고리형 백본(ring backbone)은 C₃₀₀H₆₀₀과 같고 선형 곁가지 부분(linear branch)은 C₉₆H₁₉₃개의 분자량과 같으며, 전체적으로 C₃₉₆H₇₉₃의 분자량과 같다.
Figure 2에서 보듯이, 각 올가미형 고분자 체인 시스템의 가장 긴 완화 시간(longest relaxation time)은 체인의 회전반경(chain radius of gyration)의 시간 상관 관계 함수(time correlation function, TCF)를 이용하여 계산하였다. 일반적으로 고분자 체인 시스템의 가장 긴 완화 시간은 체인의 종단 간 거리 벡터(chain end-to-end vector)나 체인의 회전반경(chain radius of gyration)의 시간 상관 관계 함수를 지수 붕괴 함수(exponential decay function)를 이용하여 추정할 수 있다. 하지만, cyclic_ 3tails 고분자 체인의 경우 종단 간 거리 벡터를 정의하기 어렵기 때문에 완화 시간을 계산하는데 체인 회전반경의 상관 관계 함수를 이용하였다. Cyclic_1tail 고분자 체인의 가장 긴 완화 시간은 14.53이고 cyclic_2tails 고분자 체인의 가장 긴 완화 시간은 33.00이며, cyclic_3tails 고분자 체인의 가장 긴 완화 시간은 23.04이다. 특히, 같은 비드 수의 고리형 백본을 가진 cyclic_1tail 고분자 체인과 길이와 cyclic_2tails 고분자 체인을 비교해 보면 선형 고분자의 배치에 따라 완화 시간이 2배 정도 차이 난다는 사실을 알 수 있다.

올가미형 체인의 분자 구조에 따라 어떠한 구조적, 동역학적, 유변학적 특성이 나타나는지 살펴보기 위해 표준 흐름 유형(standard flow type) 중의 하나인 전단 흐름(shear flow)을 이용하여 각 올가미형 고분자 체인 시스템의 특성을 비교해 보았다. 먼저, 올가미형 고분자 체인의 분자 구조에 따른 각 고분자 체인 시스템의 유체역학적 구조 변화를 살펴보기 위해 평균 제곱 체인 회전 반경(mean-square chain radius of gyration)을 전단율에 따라 조사하였다.
Figure 3(a)에서 볼 수 있듯이 자유 배수 용액 하 각 올가미형 고분자 체인은 고분자 용액 속 고분자 체인과 같은 전형적인 거동을 보여주었다.^53-55 유동 세기가 약한 낮은 전단율 영역에서 각 올가미형 고분자 체인 시스템은 매우 낮은 <R_g²> 값을 유지한다. 유동 세기가 강해지고 이로 인한 체인 스트레칭과 흐름 방향 정렬(chain stretching and alignment to flow direction)이 일어나는 중간 전단율 영역에서 각 올가미형 고분자 시스템의 <R_g²> 값은 급격하게 증가하게 된다. 유동 세기가 매우 강한 높은 전단율 영역에서는 체인의 텀블링 및 회전이 일어나며 이로 인해 각 올가미형 고분자 체인 시스템의 <R_g²> 값은 더 이상 증가하지 않고 정체 영역(plateau regime)에 도달하게 된다.
같은 전단 세기에서 cyclic_1tail 고분자 체인은 다른 고분자 체인들보다 더 높은 <R_g²> 값을 가진다. 이러한 현상의 원인을 찾아내기 위해 각 고분자 시스템을 고리형 백본과 선형 곁가지 부분으로 나누어 각각의 크기를 비교해 보았다. 고리형 백본은 크기는 고리형 백본의 지름을 평균한 지름 벡터 <R_d>
로 나타내었고, 선형 곁가지의 크기는 곁가지 부분의 종단 간 백터 <R_br>로 나타내었다. 먼저, 같은 고리형 백본을 가진 cyclic_1tail 고분자 체인과 cyclic_2tails 고분자 체인의 <R_d²>를 비교해 보면 전체 전단율 영역에서 둘은 매우 유사한 값을 가짐을 알 수 있다. 이는 cyclic_1tail 고분자 체인과 cyclic_2tails 고분자 체인의 고리형 백본 부분이 전단 유동 하에서 매우 유사하게 변형되고 있음을 의미한다. 하지만, 같은 전단 세기에서 cyclic_1tail 고분자 체인과 cyclic_2tails 고분자 체인의 <R_g²> 값은 같지 않음을 알 수 있다. Figure 3(c)에서 볼 수 있듯이, 같은 전단율에서 cyclic_2tails 고분자 체인의 br²>가 cyclic_1tail 고분자 체인의 <R_br²>에 비해 다소 짧다는 사실을 확인할 수 있다. 따라서, 올가미형 고분자 체인의 <R_g²> 값이 서로 다른 이유는 선형 곁가지 부분의 길이와 개수 및 배치에 매우 깊은 관련이 있는 것으로 보인다.
전단율에 따른 각 올가미형 고분자 시스템의 유체역학적 구조 변화는 |R_g|의 확률 분포 함수(probability distribution function, PDF)로부터 더욱 자세히 살펴볼 수 있다. 각 올가미형 고분자 체인 시스템에 대해 전단율에 따라 |R_g| PDF를 계산하였으나, 명확한 비교를 위해 세 가지 전단 세기를 선택하여 Figure 4를 완성하였다. 세 가지 전단 세기는 선형 점탐성 영역(linear viscoelastic regime), 비선형 점탄성 영역(nonlinear viscoelastic regime), 선형 점탄성에서 비선형 점탄성으로 전환되는 영역에서 선택되었으며 Figure 3(a)의 <R_g²> 그래프에서 수직선으로 표시되어 있다. 평형(equilibrium)에서 이상적인 체인(ideal chain)의 |R_g| PDF는 가우스
분포 함수(Gaussian distribution function)를 따른다.^1,2 마찬가지로, 낮은 유동 세기에서 각 올가미형 고분자 체인의 |R_g| PDF는 전형적인 가우스 분포
함수를 보여주고 있다. 전단 유동 세기가 증가함에 따라 각 올가미형 고분자 체인의 |R_g| PDF는 전형적인 가우스 분포 함수로부터 변형된다. Figure 4에서 볼 수 있듯이 각 올가미형 고분자 체인의 |R_g| PDF는 낮아지게 되고 폭은 넓어지게 되며 피크는 더 높은 |R_g|값으로 이동해 나간다. 이러한 변화는 전단 유동에 의한 ‘체인 스트레칭 및 흐름 방향 정렬’과 ‘체인 텀블링 및 회전 메커니즘’과 밀접한 연관을 맺고 있다.
올가미형 고분자 체인 시스템의 경우 고리형 백본 부분과 선형 곁가지 부분을 동시에 가지고 있기 때문에 특징적인 |R_g| PDF 거동을 보여준다. 각 올가미형 고분자 시스템은 선형 체인 부분을 가지고 있기는 하지만 고리형 백본의 영향으로 인하여 선형 고분자 체인의 전형적인 |R_g| PDF 거동을 보여주지 못한다. 다시 말하면, 각 올가미형 고분자 시스템의 |R_g| PDF에서는 고리형 백본의 영향으로 선형 고분자 체인에서 보이는 스트레칭 피크와 텀블링 피크를 관찰할 수 없다. 대신에 cyclic_1tail 고분자 체인과 cyclic_2tails 고분자 체인의 |R_g| PDF는 낮은 |R_g|값으로 치우친 모습을 보여주며 cyclic_3tails 고분자 체인의 |R_g| PDF 값은 높은 |R_g|값으로 치우진 모양을 보여준다. 하지만, cyclic_3tails 고분자 체인의 |R_g| PDF의 폭이 다른 올가미형 고분자 체인 시스템보다 좁기 때문에 컴팩트한 구조를 가지고 있다는 사실을 확인할 수 있다. 이는 Figure 3(a)에서 cyclic_3tail 고분자 체인이 다른 고분자 체인보다 다소 낮은 |R_g| 값을 가지고 있는 것과 일치한
다. 이전 연구 결과에 따르면 전단 유동에서 자유 배수 용액 하 고리형 고분자 체인은 빠른 전단 세기
에서 고리형 고분자 체인의 각 사이드가 서로 접근하여 이중 가닥(double-strained)으로 이루어진 선형 구조를 만든다고 한다.⁵⁵ 그 결과, 고리형 고분자 체인은 단일 가닥(single-strained)으로 이루어진 선형 고분자 체인과 비슷한 체인 텀블링 및 회전을 보여준다. 이전 연구에서 자유 배수 용액 하 순수 고리형 고분자 체인은 선형 고분자 체인과 비슷한 S자 텀블링(S-shape tumbling) 및 헤어핀 텀블링(hairpin tumbling)을 보여주었다.^53,54
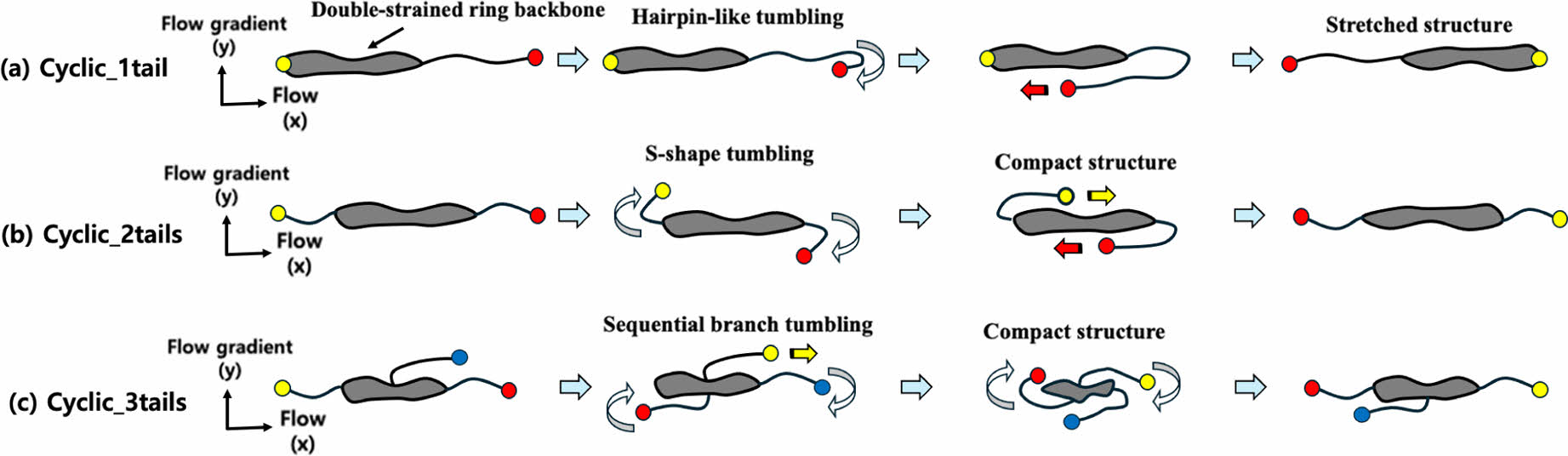
마찬가지로, 전단 유동 하 자유 배수 용액에서 올가미형 고분자 체인의 고리형 백본도 순수 고리형 체인과 매우 유사하게 이중 가닥으로 이루어진 선형 구조를 만든다. 이에 따라 올가미형 고분자 체인의 고리형 백본도 선형 고분자 체인의 텀블링과 비슷한 거동을 보여줄 것이라 예상할 수 있다. 하지만, Figure 5에서 보듯이, 선형 곁가지의 수와 길이 및 배치에 따라 선형 고분자 체인과 상이한 체인의 텀블링 및 회전 메커니즘을 보여준다. 먼저, cyclic_1tail 고분자 체인의 경우 이중 가닥으로 이루어진 선형 고분자 백본과 선형으로 이루어진 곁가지로 구성되어 있기 때문에 빠른 전단 세기에서 전체적인 체인은 흐름 방향으로 쉽게 정렬된다. 이러한 상황에서 이중 가닥으로 이루어진 선형 고분자 백본보다 자유로운 체인 끝을 가지 곁가지 부분이 랜덤하게 움직이다 전단 속도 기울기에 차이에 의해 체인 텀블링이 시작되게 된다. 체인 텀블링 과정 중에 이중 가닥으로 이루어진 선형 고리형 백본은 움직이기 어렵기 때문에 선형 곁가지 부분이 주로 텀블링을 하게 되면서 헤어핀 모양의 체인 텀블링을 주로 보여준다(Figure 5(a)). 이러한 헤어핀 모양의 체인 텀블링은 고분자 용융체에서 쉽게 관찰된다.⁵³ Cyclic_2tails 고분자 체인의 경우 높은 전단 유동 세기에서 고리형 백본을 중심으로 양쪽의 선형 곁가지 부분이 흐름 방향으로 정렬하게 된다. 이 때 자유로운 체인 끝을 가진 양쪽의 선형 곁가지로부터 체인 텀블링이 시작된다. 그러나 체인의 중간 부분에 위치한 이중 가닥으로 이루어진 고리형 백본 때문에 전체 고분자 체인은 선형 고분자 체인만큼 잘 접히지 않아 선형 고분자 체인과 같은 텀블링은 잘 일어나지 않을 것이라 예상된다. 즉, cyclic_2tails 고분자 체인은 양쪽 끝이 고리형 백본 쪽으로 접히고 고리형 백본은 선형 이중 구조를 유지하고 있는 형태를 유지할 것이라 예상된다(Figure 5(b)). 그러므로 전체적인 고분자 체인의 크기는 같은 분자량을 가지는 선형 고분자 체인보다 줄어들 것이라 생각된다. Cyclic_3tails 고분자 체인의 경우 고리형 백본을 따라 일정하게 위치한 선형 곁가지들이 높은 전단 유동 세기에서 차례대로 텀블링 하는 거동을 보여준다(Figure 5(c)). 이러한 곁가지의 순차적인 텀블링은 스타모양 고분자(star polymer)의 체인 텀블링과 유사한 측면이 있다. 선형 곁가지의 배치와 순차적인 텀블링 그리고 상대적으로 작은 고리형 백본의 크기 때문에 cyclic_3tails 고분자 체인은 다른 올가미형 고분자 체인보다 더 컴팩트한 구조를 가진다.
Figure 6에서 올가미형 고분자 체인 시스템의 유체역학적 구조 변화와 유변학적 특성을 살펴보기 위해 여러 가지 중요한 material functions을 비교해 보았다. Figure 6(a)에서 볼 수 있듯이 올가미형 고분자 체인 시스템의 전단 점도(η/η₀)는 전단율이 증가함에 따라 감소하는 전형적인 면찰 담화 거동(shear-thinning behavior)을 보여준다. 고분자 이론 및 모델에 따르면 고분자의 점도는 분자량이 증가함에 따라 증가한다. 이에 따라 같은 분자량을 가지고 있는 세 가지 종류의 올가미형 고분자 체인 시스템은 비슷한 점도를 보여줄 것으로 예상된다. 하지만, 같은 전단율에서 점도를 비교해 보면, 각 고분자 시스템들은 각기 다른 점도를 보여준다. 예를 들어, 같은 전단율에서 cyclic_1tail 고분자 시스템의 점도가 가장 낮고 cyclic_3tails 고분자 시스템의 점도가 가장 높음을 관찰할 수 있다. Cyclic_2tails 고분자 시스템은 그 사이에 위치한다. 이러한 차이는 각 올가미형 고분자 체인의 유체역학적 구조 변화와 유변학적 거동에 깊은 관련이 있다고 생각한다. Cyclic_1tail 고분자 체인의 경우 전단 유동 하에서 이중 가닥으로 이루어진 선형 고리형 백본과 선형 곁가지 때문에 흐름 방향으로 쉽게 정렬되고 스트레칭 된다. 또한, 체인 텀블링 사이클 동안 체인 백본을 따라 헤어핀 모양의 텀블링을 하기 때문에 다른 고분자 체인들과 많은 상호 작용을 하지 않는다. 선형 고분자 체인과 매우 유사한 유체역학적 구조와 유변학적 텀블링 거동은 cyclic_1tail 고분자 체인의 상대적으로 낮은 점도와 관련이 깊다. Cyclic_2tails 고분자 체인의 경우 이중 가닥으로 이루어진 고리형 백본이 선형 고분자 체인만큼 체인 텀블링 및 회전에 참여하지 않게 되고 양쪽 선형 곁가지 부분은 고리형 백본 쪽으로 접히는 구조를 이루게 된다. 이에 따라 cyclic_2tails 고분자 체인은 cyclic_1tail 고분자 체인보다 흐름 방향으로 덜 스트레칭된 구조를 가지게 되며 이러한 구조는 체인 텀블링 메커니즘에 영향을 미치게 된다. 따라서 cyclic_2tails 고분자 체인의 점도는 cyclic_1tail 고분자 체인의 점도보다 높아지게 된다. Cyclic_3tails 고분자 체인의 경우 선형 곁가지의 배치와 순차적인 텀블링 그리고 상대적으로 작은 고리형 백본의 크기 때문에 흐름 방향으로 잘 정렬되지 않은 컴팩트하고 덜 스트레칭된 구조를 가진다. 이에 따라 cyclic_3tails 고분자 체인 시스템은 다른 올가미형 고분자 체인 시스템보다 같은 전단 유동 세기에서 가장 높은 점도를 가진다.
Figure 6(b)와 (c)는 1차 및 2차 수직 응력 계수(1^st and 2^nd normal stress coefficient, Ψ₁/Ψ₁₀와 Ψ₂/Ψ₂₀)를 전단율에 따른 함수로 나타냈다. 그림에서 보듯이 자유 배수 용액 하 각 올가미형 고분자 체인 시스템들은 전단율이 증가함에 따라 수직 응력 계수가 감소하는 전형적인 면찰 담화 거동(shear-thinning)을 보여주고 있다. Figure 6(a)의 점도와 마찬가지로 같은 전단율에서 cyclic_3tails 고분자 체인이 가장 큰 수직 응력 계수 값을 보여주고 있으며 cyclic_1tail 고분자 체인 시스템이 가장 작은 수직 응력 계수 값을 가진다. 이는 앞서 설명한 바와 같이 각 고분자 시스템의 유체역학적 형태 변화와 유변학적 거동에 기인한 것이라 생각할 수 있다.
복원 탄성 응력(restoring elastic stress)과 소산 전단 응력(dissipative shear stress) 사이의 비율인 응력 비율(stress ratio, -Ψ₂/Ψ₁)은 유체의 탄성(elasticity)을 나타내는 척도이다. 일반적으로 뉴턴 유체(Newtonian fluids)의 경우 응력 비율은 0이며 비뉴턴 유체(non-Newtonian fluids)의 경우 낮은 전단율에서 0값을 보여준다.⁵⁶ 또한 응력 비율은 전단율이 증가함에 따라 단조롭게 증가하며, 폴리에틸렌의 경우 2에서 3사이의 값을 얻을 수 있다. Figure 6(d)에서 cyclic 1tail은 다른 올가미형 고분자 체인보다 높은 응력 비율을 보여주고 있고, cyclic_3tails 고분자 체인은 다른 올가미형 고분자 체인보다 상대적으로 낮은 응력 비율을 보여주고 있다. 이는 cyclic_3tails 고분자 체인의 컴팩트하고 덜 변형된 구조에서 기인하는데 이러한 구조로 인해 cyclic_3tails 고분자 체인은 낮은 탄성을 가지게 되고 그 결과 상대적으로 낮은 응력 비율을 보여준다.

선형 고분자 체인과 고리형 고분자 체인의 특성을 공유하고 있는 올가미 형태의 고분자 체인은 멀티 고리형 고분자 체인 중 가장 간단한 구조를 가지고 있다. 본 연구에서는 체계적인 거친 입자 브라운 동역학 전산모사를 이용하여 올가미형 고분자 체인의 분자 구조가 고분자의 유체역학적 구조 변화와 유변학적 거동에 어떠한 영향을 미치는지 비교 분석하였다. 이러한 분석을 위해 같은 분자량을 가지고 있지만 고리형 백본 및 선형 곁가지의 수와 길이가 다른 세 가지 종류의 올가미형 고분자 체인을 고안하였다.
일반적인 고분자 이론 및 모델에 따르면 고분자 체인의 크기는 분자량에 따라 커진다. 하지만, 세 가지 종류의 올가미형 고분자 체인들은 전단 유동 하 그 분자 구조에 따라 각기 다른 크기를 보여주었다. 고분자 체인의 크기를 나타내는 대표적인 물성인 평균 제곱 체인 회전 반경 <R_g²>와 |R_g|의 확률 분포 함수를 전단 세기에 따라 살펴보면 cyclic_3tails 고분자 체인이 가장 컴팩트하고 덜 변형된 구조를 가지고 있었으며 cyclic_1tail 고분자 체인이 가장 스트레칭된 구조를 가지고 있었다. 특히, 같은 수의 고리형 백본을 가지고 있는 cyclic_1tail 고분자 체인과 cyclic_2tails 고분자 체인의 비교 분석을 통해 고리형 백본보다 선형 곁가지 부분의 길이와 개수 및 배치가 올가미형 고분자 체인의 크기에 영향을 미친다는 사실을 밝혀냈다.
전단 유동하 자유 배수 용액에서 올가미형 고분자 체인들의 고리형 백본은 이중 가닥으로 이루어진 선형 구조를 형성한다. 이에 따라 올가미형 고분자 체인의 고리형 백본도 선형 고분자 체인과 비슷한 텀블링 메커니즘을 보여줄 수 있을 것이라 예상할 수 있다. 하지만, 선형 곁가지의 수와 길이 및 배치에 따라 선형 고분자 체인과는 상이한 텀블링 및 회전 메커니즘을 보인다. Cyclic_1tail 고분자 체인은 전체적으로 선형 고분자 체인과 비슷한 헤어핀 모양의 텀블링 및 회전을 보여주었다. 하지만, 이중 가닥 구조로 이루어진 고리형 백본이 선형 곁가지 부분보다 상대적으로 무겁기 때문에 선형 곁가지 부분은 한쪽 끝이 고정된 선형 고분자 체인의 텀블링과 비슷한 모습을 보여주었다. 이중 가닥으로 이루어진 고리형 백본과 선형 곁가지는 흐름 방향에 쉽게 정렬되었고 잘 스트레칭 되었기 때문에 cyclic_1tail 고분자 체인은 다른 올가미형 고분자 체인에 비해 높은 면찰 담화(혹은 같은 전단율에서 낮은 점도 및 수직 응력 계수)를 보여주었다. Cyclic_2tails 고분자 체인의 경우 양쪽의 선형 곁가지 부분은 전단 유동 때문에 고리형 백본 쪽으로 잘 접히게 되지만 이중 가닥으로 이루어진 고리형 백본은 잘 접히지 않아 다소 덜 변형된 구조를 보여주게 된다. 이러한 유체역학적 구조 때문에 같은 전단 세기에서 cyclic_1tail 고분자 체인보다 높은 점도 및 수직 응력 계수를 가지게 된다. Cyclic_3tails 고분자 체인의 경우 다른 올가미형 고분자보다 크기가 작은 고리형 백본을 가지고 있고 고리형 백본을 따라 일정하게 위치한 선형 곁가지들이 순차적으로 텀블링하기 때문에 다른 올가미형 체인보다 더 컴팩트한 구조를 가진다. Cyclic_3tails 고분자 체인의 이러한 컴팩트한 구조는 낮은 면찰 담화(혹은 같은 전단율에서 가장 높은 점도 및 수직 응력 계수)의 원인이 된다.
올가미 형태의 고분자들은 다양한 소재 분야 쓰이고 있을 뿐만 아니라 비슷한 구조를 지닌 생체 단백질 분자들을 쉽게 찾을 수 있기 때문에 바이오 분야에서도 그 중요성이 나날이 증가하고 있다. 본 연구에서는 올가미 형태의 고분자 체인의 분자 구조 변화로 인한 고분자 시스템의 구조적, 동역학적, 유변학적 거동들을 살펴보았고 그 원인을 분석하였다. 이러한 연구 결과는 향후 기존 고분자의 특성을 개선하고 새로운 소재를 개발하며 바이오 단백질 분자의 거동을 예측하는데 널리 활용되어질 것이라 생각한다.