The relations between rheological properties and dispersion state of polymer adsorbed magnetic particles in the dispersion are investigated to characterize the amount of adsorbed polymer. Also, the transverse susceptibility measurement as magnetic property has been performed to characterize the magnetic dispersion. Dispersions of Co-g-Fe₂O₃ nanoparticles were prepared using a binder polymer with polar groups, which adsorbed on the surface of the magnetic nanoparticles, in the molecular chains. The adsorbed layer thickness increases with decreasing particle volume fraction because of large amount of solvent penetration in the adsorbed layer resulting in the increase of the radius of gyration of the adsorbed polymer. For the magnetic nanoparticle dispersion with the volume fraction below the interaction limit, there is shear thickening in steady shear viscosity, which is resulted from the polymer bridges. According to the transverse susceptibility measurement, there are more individual particles in the magnetic nanoparticle dispersion at low volume fraction of nanoparticle.

자성입자 표면에 고분자를 흡착시켜 분산액을 제조하고 유변학적 특성과 분산 상태 사이의 관계를 조사하였다. 또한 자성입자의 분산도를 결정하기 위해 자기적 특성인 분산액의 가로축자화율(transverse susceptibility)을 측정하였다. Co-γ-Fe₂O₃ 나노입자 분산액은 자성체 표면에 흡착되는 극성 그룹을 가진 바인더 폴리머를 사용하여 제조되었고, 자성입자의 부피분율이 즐어들면 자성입자 표면의 흡착층에 많은 양의 용매 침투로 인해 흡착된 고분자의 반경이 증가하여 흡착층 두께가 증가한다. 한계상호작용 미만의 부피 분율을 갖는 자성 나노입자 분산액의 경우, 표면에 흡착된 고분자 간의 연결로 인해 전단 농화(shear thickening) 현상이 관찰되었다. 가로축자화율 측정에 의해 자성 나노 입자의 부피 분율이 적을수록 자성입자 분산도가 우수함을 알 수 있었다.

Dispersions of magnetic nanoparticles were prepared using a binder polymer with polar groups, which adsorbed on the surface of the magnetic nanoparticles, in the molecular chains. According to the transverse susceptibility measurement, there are more individual particles in the magnetic nanoparticle dispersion at low volume fraction of nanoparticle.

Keywords: polymer adsorption, magnetic nanoparticle, dispersion, rheology, binder.

This research was supported by Research Fund from Kumoh National Institute of Technology (2019-104-144).

The authors declare that there is no conflict of interest.

It is not surprising that recent advances in big data analytics and artificial intelligence have created strong incentives for businesses to accumulate information on every measurable aspect of their business.^1,2 In the field of large-scale data handling, data from large global cloud services and financial sectors are increasing rapidly. Fortunately, most of this information does not require immediate access and the safety of long-term storage is very important.^3-6 For example, Google’s data storage amount is estimated to be about 10 Exabyte, but it is difficult to cope with the storage or backup of these with a hard disk. And in these cases, recording magnetic tape is the better solution.^7-10
Recording magnetic tape consists of a magnetic coating layer and a plastic substrate. Usually the plastic substrate is poly-ethylene terephthalate (PET) and the magnetic coating is a colloid dispersion of fine magnetic nanoparticles in polymer solutions. The quality of the tape is directly related to the properties of magnetic nanoparticles. The magnetic particles retain a permanent magnetic moment causing the strong magnetic interaction between one another which results in aggregates. Since the aggregates are similar to large particles, the high frequency recording ability and the recording density of the media is diminished. The rheological properties of the magnetic ink is very important to characterize the dispersion quality of the magnetic ink and sensitive to the microstructure of the agglomerates. For poorly dispersed magnetic inks, it is expected that particles bound in agglomerates will not physically rotate in an applied magnetic field, resulting in poor recording performance through increased surface roughness and recording noise. A significant amount of research has been performed to study the rheological properties of gel-like suspensions formed by fractal aggregation with spherical particles,^11-16 which result in non-Newtonian and solid-like viscoelastic behaviors. Moreover, with their decreased average magnetic moment and magnetic anisotropy, the aggregates do not orient well with the magnetic field applied during drying, which harms the performance of the recording media. To reduce the interaction between magnetic particles and the amount of aggregates, the polymers applied provide the steric hindrance to stabilize the magnetic particle dispersions by adsorbing on the surfaces of magnetic nanoparticles.
The process of polymer adsorption on the particle surface is relatively complicated. As far as polymer adsorption concerned, polymer-surface, polymer-solvent, and solvent-surface interactions, which are determined by properties of components of the system, such as molecular structure and molecular weight of polymers, surface characteristics of colloidal particles and quality of solvents, need to be considered. In addition to these usual adsorption considerations, one of the principle problems to be resolved is the configuration of the polymer molecule on the surface. This is recognized by Jenckel and Rumbach¹⁷ who found that the amount of polymer adsorbed per unit area of the surface would correspond to a layer more than 10 molecules thick if all the segments of the chains are attached. They suggested a model in which each polymer molecule is attached in sequences separated by bridges that extend into solution. In other words, not all the segments of a macromolecule are in contact with the surface. Those segments which are in direct contact with the surface are termed “trains”; those in between and extending into solution are termed “loops”; the free ends of the macromolecule also extending into solution are termed “tail”.
For a full description of the adsorption of polymers from solutions, it is necessary to know the amount of adsorption per unit area of the surface (G) and the distribution of segments in the vicinity of the surface ρ(z) that relates to the configuration of adsorbed polymer. The knowledge of the distribution of segments in the vicinity of the surface ρ(z) is of vital importance, particularly in connection with the evaluation of the steric interaction between polymers and particles. In view of the difficulty of obtaining ρ(z), most of the information on the configuration of polymer chains at the solid/liquid interface has been derived from adsorbed layer thickness (δ) measurements.¹⁸ Thus, it is essential to know the adsorption amount of polymer and adsorbed layer thickness to probe the adsorption behavior of polymers in suspension.^19-23 Since the interaction between polymers and particles have influences in the rheological properties of the dispersion, it is reasonable to characterize the adsorption by rheological measurement. In this study, we use steady shear and oscillatory experiment to measure some related parameters. Also, the transverse susceptibility measurement as magnetic property has been performed to characterize the magnetic dispersion.

The magnetic nanoparticle in this study is Co-γ-Fe₂O₃ (JVC Co. LTD., Japan) particle with the length of 350 nm, the average aspect ratio of 6, and the density of 4.8 g/cm³. Figure 1 shows a Cryo-TEM (2000FX, JEOL LTD., Japan) image of a magnetic dispersion made with Co-γ-Fe₂O₃ particles at 5 vol%. Most particles are found in bundles of two or more because of the very strong magnetic forces and are not easily separated. To prevent the aggregate of the magnetic nanoparticle a binder polymer, MR110 supplied by Nippon Zeon Co. LTD., (Japan) was used. MR110 is a vinyl chloride acetate copolymer with, with 0.7 wt% of the sulfuric acid group, 0.6 wt% of the hydroxyl groups, and 3.0 wt% of the epoxy component. The weight average and the number average molecular weights of MR110 are M_w = 26000 g/mol and 12000 g/mol, respectively. Cyclohexanone (Merck KGaA, Darmstadt, Germany) is chosen as the solvent because of its low volatility and good solubility for the binder polymer.
Several samples with different particle volume fraction are prepared by changing the concentration of the magnetic particle while keeping the amount of MR110 and cyclohexanone constant. The dispersions are milled using Eiger Machinery Mini Mill 100 (Eiger Machinery Inc. USA) with 1.0 mm of diameter of the steel bead for 48 hours. MR110 in cyclohexanone solutions with different concentration are made to get calibration curve. The mixtures are shake 36 hours.
The rheological measurements of the magnetic particle dispersion are performed by ARES strain-controlled rheometer (TA Instruments, USA) with cone-plate geometry, 50 mm cone diameter and 0.0392 rad cone angle. The viscosity of the supernatants is measured by TA Instruments Carri-Med rheometer (USA) with cone-plate geometry. The viscosity of MR110 solution is measured by HAKKE RS100 rheometer (Thermo Fisher Scientific, USA) with coaxial cylinder geometry.
The magnetic susceptibility measurement of the dispersion was done by AC susceptometer built in the laboratory. The AC susceptometer can apply AC field in the vertical direction and DC field in the transverse direction by placing the magnetic dispersion in a pickup coil. It has been used to investigate a relationship of magnetic property and microstructure in magnetic dispersion. It consists of sample holder, pick up coil, ac coil, and dc magnets. A dispersion is placed in the pick-up coil, and initially exposed to a small ac field to move particle along ac field. Then, a transverse dc field sweep (0-1950 Gauss) is applied and the sinusoidal signal generated by the movement of magnetization in the dispersion is reported at each dc field. The amplitude of DC magnetic field was between 0 and 2000 G.

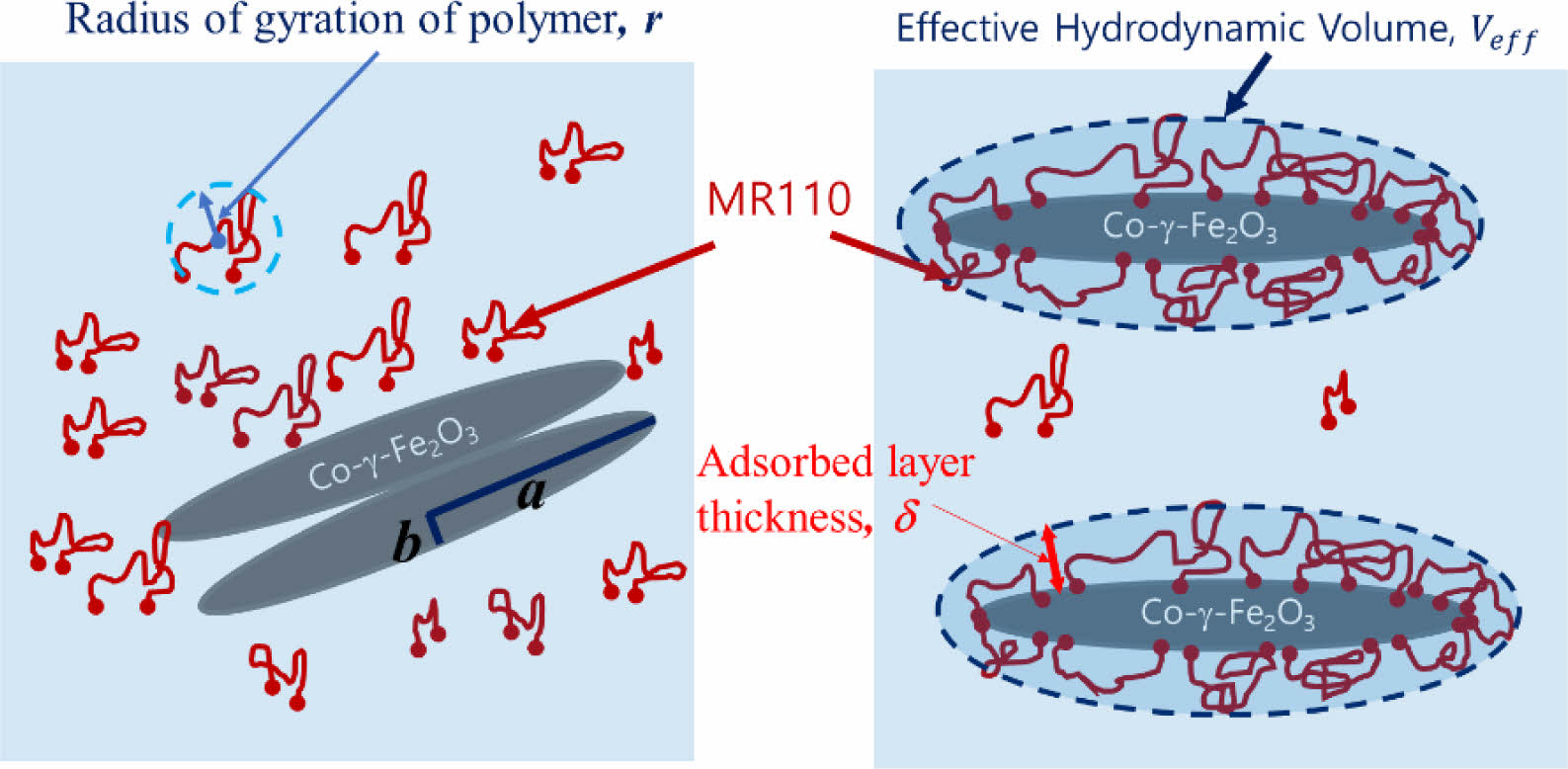
Rheological Properties of Polymer Adsorbed Magnetic Particle Dispersion. Since in the magnetic dispersion, polymers adsorb onto the particle surface and the adsorbed layer usually includes solvents, the volume of particles increases as shown in Figure 2 which shows adsorption behavior of the polymer on the magnetic particle before and after milling. The resulting particle volume fraction is called effective volume fraction (φ_eff). For the spherical particles, there is an equation relating the effective volume fraction to the adsorbed layer thickness, d, After modified by geometric consideration, the equation can be used to non-spherical particles, which is as follows.²⁴



Where, α is the half of the length of the particle and b is the radius of the particle as shown in Figure 2. Here, a/b is the aspect ratio. The thickness of adsorbed layer, δ, was obtained from commercial reference of polymer binder (MR110) and measurement of intrinsic viscosity of polymer binder solution. We adopt δ = 2 nm. Compared to the radius of gyration of the polymer, r » 13 nm, which is calculated from the molecular weight, the adsorption layer thickness is relatively small because adsorbed polymer has been stretched on the magnetic particle surface by the interaction between the polymer and the magnetic particles. We redefined the solid component consisting of the magnetic particle core and the adsorbed polymer layer shell. From the equation above, we calculated the effective volume fraction of the magnetic particles with adsorbed layer thickness.
It is well known that for all particle suspensions, the viscosity of the suspension increases with particle concentration regardless of the shear rate. For dilute suspension, the viscosity is represented by a Taylor series in the volume fraction, f, However, the series expansion becomes difficult to implement as the concentration increases. For concentrated suspensions, one obtains an equation as follows, which is achieved by Krieger and Doughty.^25,26



Here, η₀ is the viscosity of the suspending medium, φ_m is the maximum packing fraction of the magnetic particles, [η] is the intrinsic viscosity, and φ is the particle volume fraction. We made a plot of eq. (2) with the shear viscosity at infinite shear rate, η_¥, which is obtained from Casson fitting. Here we used φ_eff as a particle volume fraction in Figure 3 and determined the maximum packing fraction of the magnetic particles, φ_m as 0.46.
The interaction between the particles of a magnetic dispersion depends on the magnetization vector of each particle and the distance between the particles. At a certain distance which is called interaction limit, the magnitude of interaction diminishes about a decade. Since the volume fraction of particles is inversely related to the interparticle spacing, the interaction limit can be expressed by volume fraction of particles. And ratio of the interaction limit represented by to maximum packing fraction is 0.1.²⁷ Therefore, in our system the interaction limit of magnetic particles is 0.046 which is recalculated from eq. (2) using obtained φ_m,eff = 0.46.
And this conclusion can be confirmed by oscillatory measurement. For magnetic ink, the independence of storage modulus G' on the frequency is an evidence for the existence of structures in the system. The structure is generally referred to as some sort of association of particles as extensive as the sample itself, the association having something of the character as an elastic network.^15,16,28 It is generally accepted that the structure is formed by interaction forces in the system. Since magnetic interaction is the strongest interaction for the magnetic particles in magnetic dispersions, it is reasonable to assume that forming structures in magnetic dispersions should involve magnetic interaction. In Figure 4, G' of the inks φ_eff > 0.046 are independent of frequency, which means there are structures in those systems where the magnetic interaction between particles is still effective according to the analysis of interaction limit theory.
In Figure 5, when the particle volume fraction of the dispersion is greater than 0.034, the steady shear viscosity shows shear thinning behavior at the whole experiment range. While others show shear thickening behavior at some shear rates. Considering the adsorbed layer thickness values, the shear thickening may be resulted from bridging effect. It is generally accepted that bridging occurs when polymer chain is long enough and the surface coverage by adsorbed polymer is low. It seems that when φ≤0.046, the existence of particles does not affect the polymer configuration. According to the loop and train model,¹⁷ it is possible the train density of polymer molecules is decreased so greatly that there are only one or two contact point in a polymer molecule to the particle surface resulting in low surface coverage. At low shear rate fields, with shear rate increasing, the shear thinning behavior before onset of the shear thickening has been observed because the trapped solvent in the adsorbed layer has been released. With shear rate further increasing and more solvent squeezed out, the polymer bridges begin to extend and stretch, which generates high resistance to flow. This may explain the shear thickening behavior at moderate region of shear rates. And then at high shear rate where the suspension becomes shear thinning, the polymer bridge between the magnetic particles had been broken by high shear.
Adsorption Amount. Since viscosity of polymer solution is a function of the polymer concentration, it is reasonable to establish relation between viscosity and concentration. From the viscosity measurement of polymer solutions with different concentrations, we obtain linear calibration curve for viscosity verse concentration of MR110 solution as shown in Figure 6. According to the method of Rehacek,²⁹ the polymer adsorption amount is usually obtained by



where, Γ_ap is the apparent adsorbed amount of polymer per unit weight of particles, A₀ is the total amount of polymer and solvent per unit weight of particle, c₀ is the initial polymer weight fraction, and c_e is the equilibrium polymer weight fraction. We measured the viscosity of the supernatant for magnetic inks. From calibration curve, we got corresponding c_e. Then we calculated Γ_ap values by eq. (3). As shown in Figure 7, with particle volume fraction increasing, the polymer adsorption amount per unit weight of particles reaches a maximum then decreases. When particle volume fraction decrease, there are more particle surfaces exposed to polymer molecules resulting in the increase of the polymer adsorption amount per unit weight of particle. While the volume fraction decreases to a certain degree, the forces in the wetting process are not quite efficient because reducing loading of particles reduces the mechanical forces and temperature in the process, which negatively affect the polymer adsorption. This may be the reason that Γ_ap has maximum value. Although for the samples φ≤0.034, interaction sites per polymer molecule is reduced which we conclude from the results of the adsorbed layer thickness, there may be increase of number of molecules adsorbed on a particle because of increase in the space of interaction for polymer molecules and particles and increase of the polymer and particle ratio. This may explain that Γ_ap reaches its maximum at φ = 0.021.

Magnetic Measurement. The magnetic properties of a material can be characterized by the way in which magnetization varies with field strength. The ration of these two is called the susceptibility, c.³⁰ The susceptibility of the magnetic ink is obtained by applying an AC field to a sample that is placed vertically in a pick-up coil while detecting magnetic flux changes in the AC field direction, which results from particle and magnetization vector movement in response to the AC field. When the DC field is applied perpendicular to the AC field direction, the magnetic particles in the dispersion will be oriented producing a transverse susceptibility, χ_t. In a good magnetic dispersion, there are more single particles that are free to wiggle with the AC field giving a large χ_t and orient easily in the DC field direction resulting in a maximum χ_t at a low DC field. Poorly dispersed samples have a lot of aggregates with low net magnetic moment resulting in the restricted response to both the AC and DC field.³¹
The magnetic nanoparticle dispersion in this study is investigated by transverse susceptibility measurement. As shown in Figure 8, the magnitude of transverse susceptibility χ_t is decreased with increasing particle volume fraction, which means that the interaction between particles increase resulting less individual particles. The strong interaction for the particles in the concentrated sample is originated from the small steric barrier represented by low adsorbed layer thickness while distances between particles are reduced. When the magnetic particles are agglomerated, the magnetism is offset resulted in the uniformity of the magnetic tape is reduced after coating of the magnetic dispersion. So as shown in Figure 8 the magnitude of transverse susceptibility is decreased with increasing particle volume fraction, which means the magnetism for higher particle volume fraction is reduced by the agglomeration of particle.

It has been shown that the adsorbed layer thickness increases with decreasing particle volume fraction. The reason is that there is more and more solvent in the adsorbed layer and the train density of adsorbed polymer molecules is reduced so that adsorbed polymer molecules gain more freedom. For the magnetic dispersion, f is below the interaction limit, there is shear thickening in steady shear viscosity, which is resulted from the polymer bridges. In contrast to the decreasing train density, there is increase of number of polymer molecules adsorbed on the particles with decreasing f due to more surfaces of particles expose to polymers. From the transverse susceptibility measurement, it is concluded that there are more individual particles in the ink samples of low volume fraction.