Entanglement molecular weight is one of the key polymer properties strongly related to many mechanical and dynamic behaviors of polymers. Despite its importance, the data for entanglement molecular weight by either measurements or predictions are still far from covering a wide range of polymer species. To address this issue, we employed the deep learning technique to predict the entanglement molecular weight of polymers using graph convolutional neural networks that convert molecules into graph structures. In addition, to overcome the limitation due to the lack of data, the transfer learning technique, which transfers knowledge learned through large-scale datasets, was also introduced to improve the performance. The trained neural network model showed higher prediction performance than the conventional prediction methods.

엉킴 분자량은 고분자 사슬의 엉킴에 관한 성질로 고분자의 기계적 물성 및 동적 성질에 관련된 중요성에도 불구하고 광범위한 고분자 종에 따른 측정 데이터가 많이 부족한 실정이다. 본 연구에서는 이러한 문제점을 극복하기 위하여 심층 학습 기법을 활용하여 엉킴 분자량을 예측하고자 하였으며, 분자를 그래프 구조로 변환하여 다루는 그래프 합성곱 신경망을 이용하여 엉킴 분자량을 성공적으로 학습 및 예측하였다. 또한 데이터 수 부족으로 인한 성능의 한계점을 극복하기 위하여, 대용량 데이터를 통해 학습한 지식을 재활용하는 전이 학습 기법을 도입하여 높은 예측 성능 개선을 이루었다. 학습된 인공신경망 모델은 기존 예측 기법보다 높은 예측 성능을 보였다. 본 연구에서 사용된 기계학습 기법은 고분자 역설계 및 물성 예측 기법에 많은 도움을 줄 수 있을 것으로 기대된다.

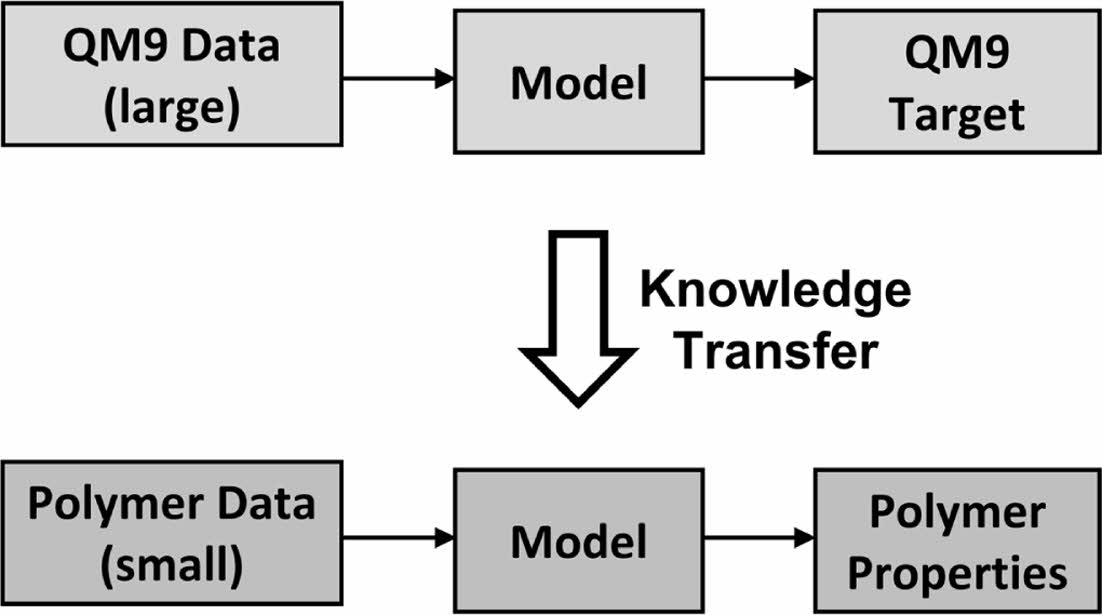
The entanglement molecular weight (M_e) for various polymers was predicted using deep learning with graph convolutional neural network. To overcome the limitation of prediction performance from an insufficient data, neural network was re-trained from the pre-trained network using the dataset of quantum chemical properties, QM9.

Keywords: entanglement molecular weight, machine learning, transfer learning, graph convolutional neural network, quantitative structure property relationship.

저자들은 이해상충이 없음을 선언합니다.

엉킴 분자량 M_e(entanglement molecular weight)는 고분자 사슬의 엉킴에 관한 고유한 성질로, 서로 이웃한 두 엉킴 점 사이 고분자 사슬의 평균적인 분자량이다.¹ 고분자 사슬의 길이가 짧을 경우, 사슬 내/간 엉킴이 발생하지 않지만 사슬이 길어질수록 엉킴이 발생하여 고분자는 다른 거동을 보이게 된다. 이는 고분자의 용융 점도(melt viscosity)와 분자량 간 관계로 나타나는데, 고분자의 분자량이 엉킴 분자량의 두배인 2M_e 미만일 경우, 용융 점도는 분자량에 선형적으로 비례하며 그 이상일 경우, 용융 점도는 분자량의 3.4제곱에 비례하여 급격히 증가하는데, M_e는 플라스틱의 다양한 기계적 물성에 관계되어 있다. 따라서 엉킴 분자량은 원하는 물성을 갖는 고분자 역설계시 고려해야 할 중요한 요소이다. 엉킴 분자량은 용융 또는 고무 상태(rubbery state)에 있는 고분자의 고원 탄성률(plateau modulus) G⁰_N을 측정, 다음 관계식을 이용하여 구할 수 있다.²



이 때, ρ는 고분자의 용융 밀도, R는 기체 상수, T 는 절대 온도이다.
그러나 이러한 중요성에도 불구하고 측정의 어려움에³ 기인하여 엉킴 분자량의 측정 데이터는 매우 부족하다. CROW사에서 운영하는 polymerdatabase에⁴ 60종 정도의 엉킴 분자량 데이터가 수록되어 있으며 최대의 고분자 데이터베이스인 PolyInfo에^5,6 엉킴 분자량 데이터가 기록되어 있지 않다. 따라서 고분자 역설계에 많은 어려움이 발생한다. 이를 극복하기 위해선 많은 측정을 통한 데이터 축적도 중요하지만, 고분자의 구조를 통하여 예측할 수 있는 예측 기법의 개발이 필요하다.
측정된 데이터를 통해 주어진 구조로부터 물성을 예측하는 구조-물성의 정량적 관계(quantitative structure property relationship, QSPR)⁷ 기법이 등장하면서 고분자의 다양한 물성도 예측하려는 시도가 있어왔다. 이 중, Van Krevelen의 group contribution method. 및 Bicerano의 topological method가⁹ 엉킴 분자량을 예측하는 방법을 기술하였으나, 다른 물성의 예측 방법과 비교하였을 시 비교적 정확도가 높지 않은 단점을 가지고 있다.
또한 4차 혁명 이후 심층 학습(deep learning) 기법이 대두되면서^10-12 고분자의 물성도 이를 통하여 예측하려는 시도가^13-17 많이 있어왔다. 데이터 수가 많은 유리 전이온도(glass transition temperature) 등의 물성은 다양한 심층 학습 기법들을 통해 매우 높은 정확도로 예측 및 보고되었다.^18-20 그러나 데이터가 매우 적은 물성들의 경우 전이 학습(transfer learning)을 이용한 시도^21,22가 보고되었으나 그 사례가 많지 않으며, 특히 엉킴 분자량은 사례가 전무하다.
심층 학습에 사용되는 인공신경망 모델은 단순한 fully-connected layer부터 합성곱 신경망까지 다양하게 제시되고 있다. 특히 그래프 합성곱 신경망은 그래프 구조를 다루는 신경망으로서 분자 구조를 다루기에 적합한 특성을 갖고 있다. 신경망 내에서 분자는 원자가 꼭짓점(vertex), 원자간 결합은 변(edge)인 무방향 그래프(undirected graph)와 같이 다루어진다. 그래프 신경망은 Monfardini 그룹에²³ 의해 발표된 이후 분자 표현에 적합한 특성에 의해 Adams 그룹에²⁴ 의하여 분자 지문(molecular fingerprints)으로 사용함에 있어 월등한 성능이 보고되었다. 이 후 DeepChem 라이브러리의²⁵ message passing neural network(MPNN)²⁶ 등 개선을 통해 QSAR 및 QSPR의 다양한 분야에 활용되어 강력한 성능이 보고되고 있다.^27,28
엉킴 분자량과 같이 데이터의 수가 적은 목표에 대해 심층 학습을 수행할 경우, support vector machine(SVM) 및 random forest와 같은 전통적인 알고리즘에 비해 더 예측 성능이 떨어짐이 일반적으로 알려져 있다.^29,30 따라서 데이터의 수가 적을 경우, 전이 학습(transfer learning)을³¹ 통해 이를 보완하는 기법이 사용된다. 전이 학습은 관련된 대용량 데이터 집합을 학습 후, 해당 학습 모델을 목표하는 학습에 재활용하는 기법으로, 소규모 데이터 집합 학습에 적합하며, 처음부터 학습하는 것보다 빠른 시간 내에 높은 예측 성능을 달성할 수 있다.
본 연구에서는 엉킴 분자량의 예측 성능 개선을 위하여 심층 학습을 이용, MPNN을 활용한 그래프 합성곱 인공신경망을 통해 CROW polymerdatabase로부터 수집한 용융 상태 고분자의 엉킴 분자량을 학습하였다. 학습을 위하여 고분자의 구조를 표현한 문자열을 인공신경망에 입력, 엉킴 분자량 값이 최종 출력되도록 회귀 지도 학습을 수행하였다. 입력된 고분자의 구조는 인공신경망에서 분자의 구조를 학습하기에 용이한 그래프 자료구조로 변환되었으며, 서로 결합된 원자-원자간 상호작용을 학습하도록 하였다. 인공신경망에서 출력된 예측 값 및 목표 값 사이의 오차를 인공신경망에 다시 역전파(backpropagation)하여, 오차를 감소시키는 방향으로 인공신경망 내의 상태 파라미터인 가중치(weight) 및 편차(bias)를 조정함으로써 엉킴 분자량을 학습하였다. 또한 적은 데이터 수로 인하여 발생하는 예측 성능의 한계를 극복하기 위하여 추가적으로 전이 학습 기법을 도입하였다. 목표 물성과 관련도가 높은 물성을 가진 대용량 데이터 집합인 QM9 데이터 집합에 대하여 먼저 학습 후, 해당 인공신경망에 고분자 구조-엉킴 분자량 데이터 집합을 다시 학습시켜 예측 성능을 높은 폭으로 개선하였다.

데이터 집합 준비. 인공신경망 학습을 위해 두가지 데이터 집합을 준비하였다. 사전 학습을 위한 데이터 집합은 QM9^32,33 데이터 집합을 사용하였다. QM9 데이터 집합은 H, C, N, O, F로 구성된 작은 유기 분자들의 성질을 양자 계산을 통해 축적한 데이터 집합으로, 총 13만개의 데이터를 가지고 있어 사전 학습에 사용할 빅데이터 집합으로 적합하다. 중복된 항목 및 라디칼을 제거 후 데이터 집합에 기록된 분자 구조를 simplified molecular input line entry system (SMILES)³⁴ 문자열로 변환하였다.
고분자의 엉킴 분자량 학습을 위하여 고분자 구조-엉킴 분자량 데이터 집합을 CROW polymerdatabase에서⁴ 수집하였으며, 해당 엉킴 분자량 데이터들은 실험을 통해 용융 상태의 고분자로부터 측정된 값이다. 엉킴 분자량 데이터들은 실험을 통해 QM9 데이터 집합이 H, C, N, O, F로만 이루어진 분자들만 수록하고 있으므로 이와의 일관성을 유지하기 위하여 반복단위의 원소가 H, C, N, O, F로만 이루어진 데이터만 사용하였으며, 총 51개의 데이터를 수집하였다. 반복단위 간의 작용기를 표현하기 위하여 반복단위를 4번 반복한 올리고머의 SMILES를 엉킴 분자량과 함께 입력-출력 데이터 집합으로 사용하였다.
분자의 그래프화. 인공신경망을 통해 학습할 수 있도록 SMILES 문자열은 분자 구조로 변환 및 문자열에서 생략된 수소 원자 추가 후, 원자는 꼭짓점, 원자-원자간 결합은 변인 무방향 그래프 G=(V, E)로 변환하였다. 이 때 V∈R^NxD는 원자 표현 행렬을, E∈R^NxNxF는 원자간 결합이 포함된 그래프 인접 행렬을 나타내며, N, D, F 는 각각 분자 내의 원자 수, 원자 표현(atom representations)의²⁶ 길이, 결합 표현(bond representations)의²⁶ 길이를 나타낸다. 원자 표현 및 결합 표현은 RDKit Python 라이브러리를³⁵ 활용, Table 1 및 Table 2와 같이 추출하였다.
인공신경망 모델. 학습에서 사용한 그래프 합성곱 인공신경망은 MPNN의^26,36,37 디자인을 이용하였으며, 인공신경망 모델의 개요도를 Figure 1에 나타냈다. 인공신경망 내에서 입력된 그래프의 원자 표현 행렬 V 는 fully-connected layer(FC) 인 특징(feature) 추출 레이어를 통해 각각 초기 원자 특징 X⁰(X^t∈R^NxL)로 변환된다.



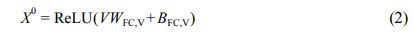
W_FC,V 및 B_FC,V는 원자 특징 추출 레이어의 가중치(weight) 및 편향(bias)를, L은 특징의 길이를 나타낸다. 그 후, 초기 원자 특징 X ⁰ 는 MPNN 모듈 내에서 직접 연결된 다른 원자로부터 발생되는 메시지 M ^t 를 통해 t < T 인 동안 반복적으로 T 번 갱신된다. u 번째 원자에 대한 t 번째 메시지 M^t_u는 MPNN 모듈 내의 NNConv²⁶ 레이어를 통해 다음과 같이 연산된다.



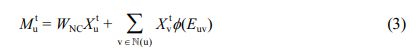
W_NC∈R^LxL는 NNConv 레이어의 가중치 행렬, N(u)는 u 번째 원자에 직접적으로 연결된 원자들의 집합이며, Φ(E_uv) → R^LxL는 결합 표현 E_uv를 결합 별 가중치로 대응시키는 함수이다. Φ(·)는 다층 fully connected layer로 구현되어 학습되도록 하였다. u 번째 원자의 특징 X^t_u는 전달된 메시지 M^t_u를 통해 MPNN 모듈 내의 GRU³⁸ 레이어에서 갱신된다.



H^t_u는 GRU 레이어의 u번째 원자에 대한 t번째 은닉 상태 (hidden state)이다. 최종적으로 분자의 특징을 나타내는 출력 특징 X̅는 전역 합 풀링 레이어(global add pooling layer)를 통해 출력된다.



분자의 특징 X̅는 다층 fully-connected layer를 거쳐 목표 물성 값 P로 출력된다. 인공신경망의 구현은 Python 라이브러리 중 기계학습 라이브러리인 PyTorch와³⁹ 그래프 인공신경망 라이브러리인 PyTorch Geometric을⁴⁰ 활용하여 구현하였다.
인공신경망 학습. 전이 학습의 효과를 비교하기 위하여 두가지 방법으로 고분자의 엉킴 분자량을 학습 후, 성능을 측정하였다. 첫번째로 전이 학습을 수행하지 않고 처음부터 고분자 구조-엉킴 분자량을 학습하였으며, 500 epoch 동안 학습하여 시험 집합 예측 성능이 가장 높았던 epoch의 모델을 이용하여 성능을 측정하였다. 두번째로 QM9 데이터 집합을 먼저 학습한 모델을 재사용하는 전이 학습을 통해 고분자 구조-엉킴 분자량을 학습하였다. 이 과정에서 사전 학습 과정으로 QM9 데이터 집합을 먼저 200 epoch 동안 학습하였다. 이 후 학습한 모델의 말단 레이어인 다층 fully-connected layer를 제외한 모든 레이어를 학습이 되지 않도록 고정(freeze) 및 말단 다층 fully-connected layer를 초기화 후 고분자 구조-엉킴 분자량으로 200 epoch 동안 학습하였다. 이후 고분자 데이터 집합에 적합하도록 모델의 미세 조정(fine-tuning)을 위하여 모든 레이어의 고정 상태를 해제한 후, 기존 학습률 (learning rate) lr의 0.01배인 0.01lr을 새로운 학습률로 설정하여 300 epoch 동안 학습하였다. 미세 조정 과정 동안 시험 집합 예측 성능이 가장 높았던 epoch의 모델을 이용하여 전이 학습 모델의 성능을 측정하였다. 학습에 사용한 최적화알고리즘(optimizer)은 Adam optimizer를⁴¹ 사용하였으며, 초 매개 변수(hyper parameter)인 학습률 lr=1e^-4, 특징 길이 L=128, 메시지 전달 반복 횟수 T=6, 배치의 크기는 16으로 설정하였다. 학습을 위한 손실 함수(loss function) 및 시험 집합에 대한 모델의 성능 평가 지표로 평균 제곱 오차(MSE, mean square error)를 사용하였다. 또한 회귀 문제를 학습하는 모델이므로 출력 값은 scikit-learn Python 라이브러리의⁴² StandardScaler를 사용, 0의 평균 및 1의 표준편차를 갖도록 표준화(standardization)하여 예측하도록 하였다.
인공신경망 성능 검증. 수집한 고분자 구조-엉킴 분자량 데이터의 개수는 매우 적으므로, 일반적인 방법을 사용하여 훈련 집합(train set) 및 시험 집합(test set)을 분리 시 모델의 성능 검증에 문제점이 발생한다. 먼저 학습 시 분리된 시험 집합에 따른 예측 성능의 편차가 매우 크며, 학습 시 인공신경망 모델이 훈련 집합에 대하여 과적합(overfitting)되어 실제 예측 성능이 매우 저하될 가능성이 크다. 따라서 모델의 성능 검증을 위하여 K-겹 교차 검증(K-fold cross validation)을⁴³ 사용하여 이러한 문제점을 극복하고자 하였다. K-겹 교차 검증에서 데이터는 집합을 서로 겹치지 않는 K개의 부분 집합으로 나뉜다. i(i∈[1,K])번째 실험에서 i번째 부분 집합을 시험 집합으로, 나머지 부분 집합을 훈련 집합으로 사용하여 총 K번 실험을 진행하였다. 이 후 총 K개의 결과를 취합하여 전체적인 성능을 평가하였으며, 피어슨 상관 계수(pearson correlation coefficient) r,⁴⁴ 평균 절대 오차(mean absolute error, MAE), 평균 제곱근 오차(root mean square error, RMSE)를 평가 지표로 이용하였다. K-겹 교차 검증 방법은 scikit-learn Python 라이브러리를 사용하여 구현하였으며, K=5로 하여 실험을 진행하였다.

데이터 시각화를 통한 학습 전략 수립. QM9 데이터 집합은 총 12 종류의 다양한 성질을 기록하고 있다. 따라서 사전 학습에 사용하기 위해 고분자의 엉킴 분자량과 상관 관계를 갖는 적합한 성질 탐색이 필요하였다. Figure 2에 나타낸 것과 같이 고분자의 물성 중 몰 부피(molar volume)가 엉킴 분자량과 상관성을 보임을 확인할 수 있었으며, QM9의 성질 중 분자의 크기와 관련 있는 전자 공간 범위(R², electronic spatial extent)가 이와 유사한 성질로 판단되어⁴⁵ 사전 학습의 목표 예측 성질로 사용하였다.
다만, Figure 2에서 확인할 수 있듯이 모든 데이터가 양의 상관 관계를 보이지 않았다. 데이터는 두개의 군집(cluster)으로 나뉘어 한 군집은 양의 상관 관계를 보였으며 다른 군집은 상관 관계를 보이지 않았다. 따라서 데이터를 나누지 않고 학습하였을 경우, 다른 군집의 데이터로 인해 학습에 악영향을 끼칠 수 있어 이를 극복하고자 데이터를 나누어 각각 학습을 진행하는 전략을 수립하였다.
데이터를 두개의 군집으로 나누기 위하여 군집 분석 (clustering analysis)을 시행하였다. OSIRIS Datawarrior 프로그램을⁴⁶ 이용하여 분자의 분자 지문을 통해 군집 분석을 수행하였으며, 사용한 분자 지문은 FragFp 설명자(descriptor)⁴⁷이다. 군집 분석을 수행한 결과, 고분자 데이터를 총 5개의 군집으로 나눌 수 있었으며, 이는 Figure 2의 마커 색깔 및 범례를 통해 나타냈다. 이를 통해 acrylate, methacrylate, ethylene 구조를 갖는 고분자 데이터를 양의 상관 관계를 갖는 펜던트 그룹으로, 나머지 데이터를 그 상관 관계를 가지지 않는 사슬 그룹으로 나눌 수 있었으며 각각의 그룹에 대하여 실험을 진행하였다.
사전 학습. 전이 학습에 사용하기 위하여 QM9 데이터 집합을 이용, 사전 학습을 수행하였다. 총 데이터 집합 중 훈련 집합으로 80%, 나머지는 시험 집합으로 나누어 학습 및 검증을 진행하였다. 목표 예측 성질인 전자 공간 범위는 데이터의 범위 및 편차가 매우 크고, 양의 값 만을 예측해야 하므로 해당 값을 그대로 학습하지 않고, 상용로그 연산을 통해 변환된 값을 학습 및 예측하도록 하였다. 그 결과, 시험 집합에 대하여 높은 예측 성능을 보임을 확인할 수 있었다. (Figure 3).
학습 결과. 사전 학습과 마찬가지로, 고분자의 엉킴 분자량은 데이터의 범위 및 편차가 매우 크고 양의 값 만을 예측해야 하므로 상용로그 연산을 통해 변환된 값을 학습 및 예측하도록 하였다. 또한 전이 학습 도입의 효과를 알아보기 위하여, 전이 학습을 하지 않은 경우 및 전이 학습을 한 경우에 대하여 고분자의 엉킴 분자량을 예측한 결과를 비교하였다. 먼저 사전 학습 데이터와 양의 상관 관계를 갖는 펜던트 그룹에 대한 학습 결과를 Figure 4에 나타냈다. 펜던트 그룹의 경우 전이 학습 여부에 관계없이 높은 예측 성능을 보여주었으나, 전이 학습을 수행하였을 때 모든 지표에서 더 높은 예측 성능을 보여주었다. 따라서 사전 학습에서 유사한 성질을 학습, 전이되는 지식을 이용하여 본 학습에 도움을 받을 수 있음을 확인하였다.
사전 학습 데이터와 상관 관계를 갖지 않는 사슬 그룹에 대한 학습 결과를 Figure 5에 나타냈다.
전이 학습을 하지 않은 경우, 피어슨 상관 계수 r=0.2147로서 분자 구조에 관계없이 비슷한 값을 예측, 낮은 예측 성능을 보였다. 이는 펜던트 그룹의 경우 주쇄의 구조가 비슷하여 학습이 비교적 수월한 반면, 사슬 그룹은 매우 다양한 구조를 가지고 있어 적은 데이터 수로는 학습에 어려움을 겪었기 때문으로 해석된다. 그러나 전이 학습을 수행한 경우, 전이 학습을 하지 않은 경우에 비하여 월등히 예측 성능이 개선되었다. 사슬 그룹의 목표 물성 데이터는 사전 학습 시 사용한 목표 물성 데이터와 상관 관계를 보이지 않음에도 전이되는 지식이 본 학습에 도움을 주었는데, 이는 사용한 인공신경망 모델의 구조적 특성 때문으로 해석된다. 사용한 인공신경망 모델은 그래프 합성곱 인공 신경망인 MPNN 모듈 및 말단의 다층 fully-connected layer 두가지로 나뉘어진다. MPNN 모듈에서는 입력된 분자로부터 분자 구조를 학습하며, 다층 fully-connected layer에서는 MPNN 모듈에서 출력되는 값과 최종 출력 값 사이의 관련성을 학습한다. 따라서 설령 출력 데이터의 상관 관계가 부족할지라도, MPNN 모듈에서 학습하는 분자 구조는 화학 공간(chemical space) 내의 일반적인 지식으로 취급되어 전이 학습 시 도움을 줄 수 있다. 그럼에도 불구하고, 펜던트 그룹의 경우에 비하여 떨어지는 예측 성능은 적절한 상관 관계를 가지는 대리 물성(proxy property) 설정의 중요성을 보여준다.
기존 예측 방법과의 비교. 기존에 널리 사용되던 예측 방법과의 예측 성능 비교를 위하여 Bicerano의 topological method를⁹ 이용하였다. 해당 방법을 이용하여 예측한 고분자의 엉킴 분자량을 대조군으로 설정, 비교 결과를 Figure 6에 나타냈다. 인공신경망 학습 결과는 펜던트 그룹 및 사슬 그룹의 결과를 통합하여 그래프에 도시하였다. Topological method와 비교하였을 시 전이 학습을 하지 않은 경우 예측 성능이 떨어졌지만, 전이 학습을 사용한 경우 모든 지표 측면에서 예측 성능이 개선됨을 확인하였다. 또한 topological method를 사용하여 예측하였을 때 비교적 낮은 엉킴 분자량을 갖는 고분자에 대해서는 예측 성능이 좋지 않았으나, 전이 학습을 사용하였을 경우 모든 값 범위에서 좋은 예측 성능을 보여주었다.

그래프 합성곱 신경망에 전이 학습을 도입하여 매우 적은 데이터 수를 가지는 용융 상태 고분자의 엉킴 분자량을 높은 성능으로 예측하였다. 먼저 MPNN 모듈을 기반으로 한 그래프 합성곱 신경망을 통해 엉킴 분자량을 성공적으로 예측하였다. 이후 엉킴 분자량과 연관을 가지는 대용량 데이터 집합을 통해 사전 학습을 수행한 뒤, 엉킴 분자량에 대해 전이 학습을 수행하여 예측 성능을 큰 폭으로 개선하였다. 특히 사슬 그룹 데이터에 대한 전이학습 사례로 미루어 보아, 직접적인 연관성을 갖지 않는 데이터라도 화학 공간에 대한 일반적인 지식 전이를 통하여 목표 학습에 많은 도움을 줄 수 있음을 확인하였으며 이는 분자 구조를 직접적으로 학습하는 MPNN 모듈에 의한 효과로 해석된다. 전이 학습을 수행한 결과, 기존 사용되던 topological method에 비해서도 높은 예측 성능을 보였으며, 전 데이터 범위에서 고른 예측 성능을 보였다. 본 연구에서 사용한 엉킴 분자량 데이터는 용융 상태로부터 측정된 데이터에 한정되어 있으나, 온도 또는 용액의 농도 등에 따른 엉킴 분자량을 추가적으로 수집 및 학습한다면 다양한 조건에 따른 엉킴 분자량도 예측할 수 있을 것으로 생각된다. 따라서 본 연구는 원하는 물성을 갖는 고분자의 역설계에 많은 도움이 될 것으로 생각되며, 데이터 수가 적은 다른 성질의 예측 전략 수립에도 많은 기여를 할 것으로 기대된다.