This study investigated the damage mechanism of acrylonitrile-butadiene styrene (ABS)/poly(methyl methacrylate) (PMMA)/nano-SiO₂ composites. The distortion and fracture behavior of ABS/PMMA/nano-SiO₂ composites were predicted by developing the homogenization theory and the surface-based cohesive method. This model simulated the elementary action of elastoplastic damage in the matrix, the fracture for the nano-SiO₂ reinforcement, and traction separation for interfaces. The experiment and morphology of the fracture section were validated by the modeling results. The damage mechanisms of ABS/PMMA/nano-SiO₂ composites were researched with the numerical results, and the roles of nano-SiO₂ strength in the mechanical properties of ABS/PMMA blends were discussed in detail.

A microstructure-based the homogenization theory and the surface-based cohesive method was developed to predict the deformation and fracture behavior of acrylonitrile-butadiene styrene (ABS)/poly(methyl methacrylate) (PMMA)/nano-SiO₂ composite. The constitutive behavior of the elastoplastic-damage in the matrix, the fracture for the nano-SiO₂ reinforcement, and the traction-separation for interfaces, were simulated in this model.

Keywords: acrylonitrile-butadiene styrene/poly(methyl methacrylate)/nano-SiO₂ composites, damage mechanics, representative volume elements.

The authors sincerely acknowledge the financial support by the Natural Science Foundation of Shandong Province (grant no. ZR2020KF024), Yantai City Science and Technology Plan Project (grant no. 2022ZDCX016), the University Research Project of Shandong Province (grant no. J17KB007), and Natural Science Foundation of Shandong Jiaotong University (grant no. Z201937).

The authors declare that there is no conflict of interest.

Acrylonitrile-butadiene styrene (ABS), a kind of rubber-toughened thermoplastic, has been extensively applied in numerous fields for many years, such as automotive and household appliance industries, due to its excellent fabricability, low water absorption, and high impact strength. Neat ABS materials often have weak toughness and surface glossiness. Polymer blends have aroused great interest recently because these materials have excellent properties at low cost. ABS/poly(methyl methacrylate) (PMMA) blends have excellent integration of physical properties, including great surface glossiness, easy fabricability, and high mechanical strength. However, the blends’ toughness is low due to the inborn brittleness of PMMA.^1-6 The polymeric matrix cannot be toughened and stiffened simultaneously through physical blending.
To date, considerable attention has been paid to the application of inorganic nanoparticles as modifiers for the refinement of the morphology of polymer blends. Compared with traditional microcomposites, the large interfacial region and high surface energy of nanoparticle fillers have resulted in a massive surface to volume proportion of nanoparticles; these features have led to high interfacial adhesion between the polymeric matrix and fillers, influencing the properties of the total composites.⁷ Two methods have been used in research on the mechanical action of polymers modified with nanoparticles: experimental approach and numerical modeling. The roles of nanoparticles in polymer blends have been described by extensive experimental research.^8-14 After investigating the roles of SiO₂ in the morphology of micro PMMA, Mu et al.¹⁵ observed that nano-SiO₂ particles can grow on PMMA microspheres. The roles of ABS and nano-SiO₂ with various nanoparticle scales and different loadings were researched by Haghtalab and Rahimi.¹⁶ After investigating nano-CaCO₃ on the rheological and mechanical properties of ABS/PMMA blends, Zhang et al.⁸ observed a slight decrease in tensile yield strength with the growth in the nano-CaCO₃ content, and the Izod impact strength was significantly decreased by all nano-CaCO₃ particles. In our previous study, we investigated the influence of nano-SiO₂ particle modification on the morphology and properties of ABS/PMMA polymer blends. When the contents of the nano-SiO₂ fillers were less than 2 wt%, the toughness of the ternary blends was greatly enhanced.¹⁷ These studies proved that the nanoparticle surface area is enhanced by nanoparticles and great filler loadings, and polymer chain adsorption on the nanoparticles increases to intensify the viscoelastic properties. However, the actual interactions occurring among the polymer matrix, modifier, and interfaces during distortion and fracture cannot be characterized by the experimental approach.
For numerical modeling of polymer nanoparticle composites, two popular methods are commonly used: discrete element approach (DEM) and finite element approach (FEM). The DEM model shows a quicker convergence rate than FEM, but several significant elements required for the research on distortion and fracture mechanisms in polymer nanoparticle composites are neglected, including the geometry of the particles and the brittle fracture between the matrix and particles. The microstructure of the composite materials is fully reconstructed with FEM, including the irregular morphology of the particles, inhomogeneous spatial distribution of particles, and anisotropic nature in the particles. In the literature, some efficient numerical models based on FEM were adopted to research the mechanical properties of polymer composites. For instance, VuBac et al.¹⁸ quantified the key-input coefficient affecting the Young’s modulus of polymer (epoxy) clay nanocomposites by proposing a stochastic framework based on sensitivity analysis. All stochastic approaches forecast that the core coefficients for Young’s modulus are the epoxy stiffness and clay volume fraction. Pontefisso et al.¹² developed a novel algorithm for the production of 3D representative volume elements (RVEs); the algorithm is simple to be meshed and imported in an FE code. The interphase thickness and nature on the elastic nature of nanocomposites were studied via computational analysis. Yuan¹³ researched the roles of nanofiller content on the interfacial properties of polymer blend nanocomposites via micromechanical modeling of experimental tensile strength and modulus. The calculated outcomes showed excellent interfacial properties in the samples with low nanofiller concentrations.
Despite past research on the fracture action of composites via FEM, researchers were unable to determine the role of nanoparticle morphology in the properties of ABS/PMMA/nano-SiO₂ polymer blends. Given that these models are constructed based on spherical particle conception, the multiphase failure of particles was not considered in these models. The remainder of the paper is organized as follows. In Experimental section, the homogenization theory and cohesive approach based on the surface are described briefly. This section describes the materials and experimental procedures. Results and Discussion section presents a microstructure-based FEM to forecast the interfacial debonding of ABS/PMMA/nano-SiO₂ polymer blends. We also validated the model by challenging it with experimental data in this section. Some conclusions and potential extension are discussed in Conclusions section.

Micromechanical Design Theory Guidelines. Homo- genization Theory: The homogenization theory is widely used in converting inhomogeneous composite into homogeneous material. It often simulates the response of samples discretely with four-node quadrangle factors and three-node triangular factors relying on the finite element approach. The definition of four margins of RVE as periodic border conditions is made. For the minimal role of the mesh density, it was kept very fine.
The equal elastic constant tensor of composite (C_ijkl) is as follows:



where σ̅_ij is the mean stress, and ε̅_i is the mean strain of a unit cell. σ̅_ij and ε̅i _j are calculated as follows:



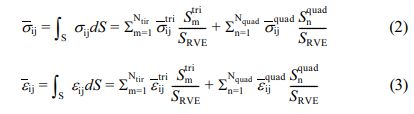
where N_tri, N_quad, means the number of triangular (quadrangular) elements, 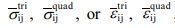, means the mean stress or strain in a triangular (quadrangular) element, 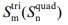refers to the area of triangular (quadrangular) element, and S_RVE refers to the total area of RVE.
The values at each Gaussian integral point in the factor are associated with the mean stress and strain of one element. Only one Gaussian integral point without coordinative transformation exists in a triangular element; therefore,



where 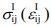means the related value of the Gaussian integral point.
In a quadrangular element, 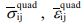can be solved by



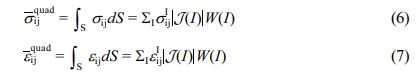
where W(I) = 1, and J(I) is the Jacobian matrix, which is expressed as



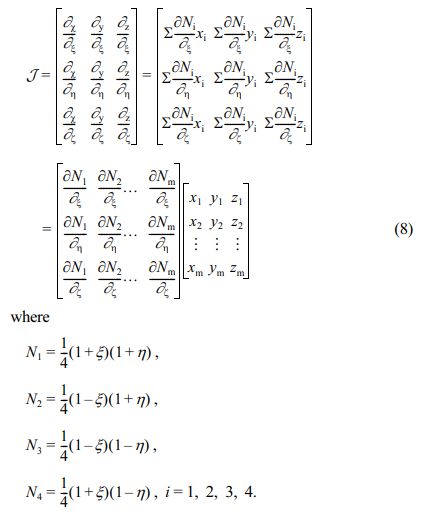
Therefore, the mean stress and strain of an overall RVE can be calculated by Eqs. (2) and (3).
Surface-based Cohesive Method: Cohesive technology is extensively used to simulate the damage between filler particles and matrix.¹⁹ This paper introduces a similar approach called surface-based cohesive action for the simulation of particles. A damage model composed of two components, namely, a damage beginning standard and a damage evolution law, is established to simulate the regression and final failure of the bond between two surfaces. This paper uses a typical traction isolation response to simulate the damage between the nano-SiO₂ particles and matrix (Figure 1). Linear elastic behavior followed by the initiation and evolution of damage is assumed in the traction separation model. Elastic behavior is written with regard to an elastic elementary matrix, which associates the normal and shear stresses with the normal and shear isolations across the interface. Elastic behavior can be written as



where t is composed of two components t_n and t_s, which refer to normal and shear traction, respectively. The related separations are denoted by δ_n and δ_s. The matrix K is a constant before damage is initiated, which will decline following the damage evolution law when damage begins.
The damage initiation criterion in this paper is the maximum stress standard. Damage begins when the largest contact stress amounts to the largest stress. This standard can be written as



where t_m^max and t_s^max are the peak values of contact stress, respectively. The symbol < > is the Macaulay bracket.
When the interface displacement reaches δ_n^max, damage evolution is adopted to soften the bond between two surfaces. The damage affects the contact stress components as follows:



where D means a scalar damage variable referring to the overall damage at the contact point. For linear softening, D is reduced to the expression below:



where the subscript “n” means the normal or shear direction, and δ_n^max represents the maximum value of the efficient separation attained in the loading history.
Materials and Experimental Procedure. Materials: Zhenjiang Chimei Chemical Co., Ltd. and Taiwan Chimei Chemical Co., Ltd. provided the ABS (757 K) and PMMA (CM-211) resins, respectively. Hangzhou Wanjing New Material supplied nano-SiO₂ (VK-SP15C). The nano-SiO₂ particles showed a mean diameter of about 15 nm. Jinan Xingfeilong Chemical Reagent Factory offered stearic acid and silane coupling agent.
Preparation of Blends: All materials were dried at 80 °C for 12 h in an air-circulating oven before application. ABS/PMMA/nano-SiO₂ was prepared with a two-screw extruder (L/D ratio: 40; diameter: 21.7 mm; SJSL-20, China) at 200-225 °C from the hopper to the die. The 12 h secondary drying of pellets was performed in an air-circulating oven at 80 °C. The standard testing specimens were processed in a 68-ton injection molding machine (XL680, China). The injection temperature was set at 225-215 °C from the hopper to the nozzle, and the holding pressure was 50 MPa. The mass ratio of ABS to PMMA was maintained at 80/20, and the content of nano-SiO₂ was 4 wt%.
Characterization: The tensile properties were performed on a CMT 5305 electrical testing machine at room temperature. The crosshead speed was kept at 4 mm/min.
Scanning electron microscopy (SEM). The broken pieces were used as SEM samples for morphological and fracture mechanism analyses after the mechanical tests. The fracture surface was coated with a thin layer of gold before observations under a FEI-NOVA NANOSEM 450 SEM.
Transmission electron microscopy (TEM). TEM (JEM-2100) was carried out to examine the morphological structure at an increasing voltage of 200 kV. The specimens were dried with a mixture of sulfur, zinc stearate, and promoter (content proportion: 90/5/5) in an oven at 120 °C. Subsequently, 100 nm-thick samples were prepared through ultra-cryomicrotomy at -100 °C with a Leica UCT microtome.

Finite Element Model. In this paper, the selected composite microstructure was represented with an RVE. The morphology of ABS/PMMA and ABS/PMMA/nano-SiO₂ blends is shown in Figure 2, which was determined by TEM. The rubber particle morphologies were regular and circular, whereas the particle morphologies of nano-SiO₂ were irregular because of aggregation.
The structure of the ABS/PMMA/nano-SiO₂ composite was modeled based on this information. Given that the minimum precise RVE size is laborious to determine, the RVE size applied is reasonable in this paper. The size of the RVE model was 1 mm × 1.2 mm, and the mean size of the rubber particles was 0.2 mm. The size and shape of nano-SiO₂ were simplified because of aggregation. The RVE model of ABS/PMMA/nano-SiO₂ is shown in Figure 3(a). The model produced is special because no particles cross the surface, which is the limitation for surface-based cohesive factor in Abaqus to imitate the ABS/PMMA/nano-SiO₂ composite. With regard to finite element discretization, the matrix and nano-SiO₂ particles were meshed by using the general linear solid element C3D8R in Abaqus. The interface behavior between matrix and particles was explained by adopting the surface-based cohesive element. The meshing of representative volume unit is shown in Figure 3(b)-(d).
The parameters of cohesive behavior and damage should be selected before using surface-based cohesive to define the boundary condition. In this paper, the above parameters were provided based on the relevant literature,^20-23 because such parameters are difficult to define. These parameters are listed in Table 1. Meanwhile, we only considered the elastic stage of nano-SiO₂ because of its high yield strength and elastic modulus relative to PMMA and ABS. PMMA and ABS were input corresponding to elastic and plastic properties, respectively.
Numerical Results and Discussion. Simulation Analysis of RVE: Figures 4 and 5 show visible stress and strain evolution, and cracks were produced and spread inside the composite during tensile loading. Analysis of the numerical model revealed that the first fracture behavior occurred between nano-SiO₂ particles and matrix when e was 0.05, and the damage area became larger with increasing e.
In this simulation, we found that the initial stage of high stress area occurred at the interface between nano-SiO₂ particles and matrix. During composite deformation, the aggregated nano-SiO₂ particles acted as stress concentration points (Figure 4). When e was 0.075, a high stress area formed in the equator of rubber particles. The high stress area of rubber particles gradually expanded from the rubber equator to the poles with the increase in the extension area. Thus, rubber particles caused further interface debonding behavior between the matrix.
Figure 5 presents the different stages of the equivalent plastic strain with increasing load. The plastic deformation zone started from the interface between the nano-SiO₂ particles and matrix. The deformation area demonstrated mutual connection under the influence of adjacent nano-SiO₂ aggregation. The connection road was along the 45° direction.
Easy interface debonding was promoted by the aggregation of nano-SiO₂ and weak interface bonding with the matrix, which declined the stiffness and strength of the ABS/PMMA/nano-SiO₂ composite. The SEM micrograph in Figure 6 displays the morphology of an actual fracture sections of ABS/PMMA/nano-SiO₂ and ABS/PMMA, in which the fracture direction was about 45°. This result was consistent with the direction observed in the numerical model.
Model Validation: The numerical model was validated by comparing the stress-strain curve predictions with the experimental response. Figure 7 presents the experimental and simulation-based stress-strain curves for ABS/PMMA/nano-SiO₂ composites. The results demonstrated that the elastic modulus, yield stress, tensile strength, and elongation of the composites predicted by the RVE model agreed well with the experimental values.
In Figure 7, the experimental and simulation-based curves showed obvious elastic-plastic behavior. The stress-strain curves for the ABS/PMMA/nano-SiO₂ composites were almost linear with the smallest elongation, compared with those for the ABS/PMMA composites. The elastic modulus of the ABS/PMMA/nano-SiO₂ composites was higher but tensile strength was lower compared with those of the ABS/PMMA composites.
In our previous study, we found that the tensile strength of the nanoparticle-filled polymer resin was less than that of pure resin.¹⁷ Nanoparticles often aggregate, leading to poor interface bonding, so they are easily pulled from the composition. The mechanical properties of nano-SiO₂ were obviously different from those of the matrix, and nano-SiO₂ was likely to cause interface damage. As a result, the nano-SiO₂ fillers increased the stiffness of the ABS/PMMA composites and reduced the strength and toughness of the ABS/PMMA composites.

The distortion and fracture behavior of ABS/PMMA/nano-SiO₂ composites were predicted by developing a microstructure-based finite element model. The agreement of the fracture surface morphology with those forecast by the simulation was adopted to justify the validity of the modeling results. A visible process of elasto-plastic deformation along with crack generation and propagation was described, which is helpful for research on deformation and fracture mechanisms in ABS/PMMA/nano-SiO₂ composites. Several salient highlights from our work are summed up below: (1) Tensile fracture in the ABS/PMMA/nano-SiO₂ blends is initiated by nano-SiO₂ particles, which are debonded from the matrix because of stress concentration. (2) Easy interface debonding is promoted by weak interfaces but decreases the composite’s stiffness and strength. (3) Nano-SiO₂ particles lead to fracture along the 45° direction. Thus, the simulation results are consistent with the experimental result.