Aggregates of multi-walled carbon nanotubes (CNT) were microscopically analyzed using elastic properties of their dispersion. Scaling theories based on the dependency of elastic modulus and yield stress on the CNT concentration were applied to the aggregated CNT particles suspended in ethylene glycol mixed with a polymeric dispersant. Using the scaling theories, we obtained structural parameters including fractal dimension of the aggregates. As milling time for CNT dispersion increases up to 120 min, the fractal dimension of the aggregates continuously decreases from 1.92 at 30 min to 1.28 at 120 min. This means that entangled shape of aggregates is turning into one dimensional linear shape as the dispersion time increases. It was found that overall trend of other structural parameters, rheological properties, and electrical conductivity with the dispersion time agreed with that of the fractal dimension.

다중벽 탄소나노튜브(CNT) 분산액의 탄성적 성질을 이용하여 CNT 입자의 미시적 응집구조에 대해 분석하였다. CNT 입자를 고분자 분산제가 혼합된 에틸렌글리콜에 분산시켜 얻은 분산액에 대해 저장 탄성률과 항복응력의 입자 농도 의존성에 관한 스케일링 이론을 적용하여 응집체의 프랙탈 차원를 비롯한 응집구조 변수들을 구하였다. CNT의 분산이 120 분까지 진행되면서 프랙탈 차원이 분산시간 30분일 때 1.92로부터 120분에서 1.28까지 지속적으로 감소하는 경향을 보임으로써 CNT 응집체가 엉겨 있는 형태에서 1차원적 선의 형태로 변해가는 것으로 나타났다. 다른 미시적 구조 변수들, 유변학적 물성과 전기전도도의 분산시간에 따른 변화도 프랙탈 차원의 변화에 부합하는 결과를 보였다.

Aggregates of multi-walled carbon nanotubes (CNT) were microscopically analyzed using scaling theories and viscoelastic properties of their dispersion. It was found that overall trend of other structural parameters, rheological properties, and electrical conductivity with the dispersion time agreed with that of the fractal dimension of the aggregates in the dispersion.

Keywords: carbon nanotubes, rheological properties, fractal dimension, dispersion, scaling theory.

본 연구는 2019-2020학년도 상명대학교 교내연구비를 지원받아 수행하였으며 이에 감사드립니다.

저자들은 이해상충이 없음을 선언합니다.

탄소나노튜브(CNT)는 뛰어난 전기 전도성과 열 전도성 그리고 기계적 강도를 지녀 고분자 소재의 물성을 보강하는 기능성 첨가제로 사용되고 있다. CNT가 가지는 이러한 장점에도 불구하고 큰 반데르발스(van der Waals) 힘이나 섬유상 구조로 인해 응집이 쉽게 발생하거나 분산이 어려워 CNT의 뛰어난 물성을 구현하는데 제약 요인으로 인식되고
있다.¹ CNT 입자의 분산성을 높이기 위한 방법을 효과적으로 찾아내기 위해서는 입자의 분산 혹은 응집상태에 대한 정확한 평가가 필수적이다. 일반적으로 입자 분산액의 경우 광산란이나 전자 현미경을 이용해 입자들의 분포 상태를 관찰하는데 광산란법의 경우 분산액의 농도를 극히 희석해야 하며 전자현미경을 사용하면 분석범위가 매우 국부적이고 또 액상 시료를 고체상으로 변환해야 하므로 분산액 상태 그대로의 입자 분산 상태를 관찰할 수 없다는 단점이 있다. 분산액의 상태 변화없이 분산상태를 가늠할 수 있는 방법 중 하나가 유변학적 거동을 관찰하는 것이다. 전단 점도나 복합 점도의 변화, 항복응력 혹은 탄성적 성질의 변화 경향을 관찰하는 것인데 이러한 유변학적 성질의 경향성만으로 응집 자체에 대한 미시적인 해석을 하기에는 부족한 점이 있다.
입자의 응집에 대한 좀 더 미시적이고 정량적인 해석을 위해 프랙탈(fractal) 이론을 이용할 수 있다. 자기 유사성(self-similarity)의 프랙탈 개념을 콜로이드 입자 응집에 도입하면서^2-4 많은 후속 연구가 이루어져 왔는데 그 중에서 주목할 만한 결과 중의 하나로 Shih 등의⁵ 이론을 꼽을 수 있다. 그들은 고분자 젤(gel)의 스케일링(scaling) 개념을 콜로이드 젤에 응용하여 입자 분산액의 탄성적 성질이 보이는 농도의존성에 관한 스케일링 이론을 제시하였다. 이 이론은 응집체의 프랙탈 차원(fractal dimension)을 포함한 미시적 구조 변수들을 구할 수 있게 함으로써 입자분산계에 폭넓게 활용되고 있다. 이 이론에서는 응집체의 프랙탈 차원뿐 만 아니라 응집체가 외부로부터 힘을 받을 때 그 힘이 직접적으로 전달되는 응집체내 중추(backbone)의 프랙탈 차원도 구할 수 있다. 그러나 실제 분산액에서 이 중추의 프랙탈 차원이 음수가 나오는 비현실적인 결과를 나타내는 한계를 보이기도 했는데 이는 이 이론이 응집의 패턴이 크게 강한 결합 영역(strong-link regime)과 약한 결합 영역(weak-link regime)의 두 가지 영역 중 하나에 해당된다고 지나치게 단순화시킨 데 기인한다 할 수 있다. Wu와 Morbidelli는⁶ 이러한 결점을 보완하여 두 영역 사이의 중간 영역에 대해 고려해 줌으로써 Shih 등의 이론을 좀 더 일반화하였다. 이 일반화된 이론을 CNT의 분산액에 적용한 예가 있는데 Khalkhal과 Carreau는⁷ MW-CNT와 에폭시 수지 분산계에서 점탄성 측정시 흐름 이력이나 온도가 프랙탈 차원에 미치는 영향을 분석하였으며 Urena-Benavides 등⁸은 분산성을 높이기 위해 표면처리가 된 다중벽(MW)-CNT와 불포화 폴리에스터 용액 분산계에서 CNT 입자의 벽(wall) 구조와 표면 처리 유무에 따른 유변학적 물성의 차이를 제시하고 있다.
본 연구에서는 CNT 분산액의 분산 상태 변화에 따라 응집체의 미시적 구조 변수들이 어떻게 변하는지 살펴보고자 한다. 분산상태의 변화를 주기 위해 분산시간을 달리하면서 분산액을 취해 유변학적 물성을 측정하였다. CNT 분산액의 분산시간에 따른 유변학적 거동에 대한 연구로는 Huang 등과⁹ Kim과 Choi의¹⁰ 연구를 들 수 있는데 이들은 모두 분산시간에 따른 동적 점도나 항복응력 또는 저장 탄성률의 변화를 관찰한 것으로 프랙탈 차원과 같이 응집체의 응집 정도를 정량적으로 나타내지는 않았다. 이들 선행 연구에서 다루지 않은 미시적 응집 구조 변화를 정량적으로 다루기 위해 본 연구에서는 분산시간별로 여러 농도의 분산액의 유변학적 물성을 측정하고 분산액의 탄성적 성질과 관련되는 스케일링 이론을 이용해 프랙탈 차원을 비롯한 여러 응집체 구조 변수를 구하였다. 이를 통해 분산시간에 따른 분산상태에 따라 응집체의 상태가 정량적으로 어떻게 변하는지를 알아보았다. 입자 응집에 대한 미시적이고 정량적인 분석 방법은 CNT 분산액 뿐만 아니라 다양한 입자 분산액에 응용될 수 있다.
구체적으로 먼저 입자분산액에서 CNT 분산액의 농도에 따른 저장 탄성률이나 항복응력 거동을 이용해 프랙탈 차원 등의 구조 변수를 구하는 방법에 대해 설명하고 각 분산시간에서 농도별 유변학적 물성 및 응집구조 변수를 구하였다. 이를 통해 분산시간에 따라 변하는 응집구조의 변화를 알아보았다. 미시적 응집구조 변수와 함께 유변학적 물성과 분산액의 전기전도도의 변화도 비교하였다.

시료 준비. 다중벽(MW, multi-walled)-CNT, 에틸렌글리콜(ethylene glycol), 고분자 분산제로 구성되는 CNT 분산계를 제조하였다. MW-CNT 입자로는 벨기에 Nanocyl사의 NC 7000 제품을 사용하였다. 평균 직경은 9.5 nm이고 길이는 1.5 mm로 직경 대 길이비는 대략 158이다. Figure 1의 주사 전자현미경 사진으로 입자의 이미지를 나타냈다.
이 CNT를 에틸렌글리콜과 고분자 분산제의 혼합액에 분산시켜 제조하는데 에틸렌글리콜은 일본 Junsei 화학 제품으로서 25 ^oC에서 점도가 0.017 Pa∙s 밀도가 1.10 g/cm³이며 뉴톤 유체의 성질을 띤다. 고분자 분산제로는 트윈 80(Tween 80)으로 알려진 polyoxyethylene sorbitan monooleate(C₆₄H₁₂₄O₂₆, 몰질량 1310 g/mol, 밀도 1.10 g/cm³, 덕산약품, 한국)를 사용하였다. 분산액 중 CNT 부피 농도는 0.31-0.62%의 범위이다.
CNT 분산액을 만들기 위해 먼저 약 1 g의 CNT입자를 에틸렌글리콜 10-15 mL로 약 5분간 스파츌라(spatula)를 이용해 적신 후 에틸렌글리콜과 트윈 80 혼합액을 투입했다. 트윈 80은 CNT입자 100 g에 대해 3 g의 비율로 사용하였다. 혼합된 원료 물질들의 분산 효율을 높이기 위해 밀(mill) 분산 이전에 균질기(homogenizer, 모델 HG-15D, 대한과학, 한국)를 사용하여 3000 rpm에서 1분간 균질 처리하였다. 이렇게 처리된 액을 3 mm 지름의 지르코니아 볼로 채워진 폴리에틸렌 병에 옮겨 담는다. 이 때 지르코니아 볼이 차지하는 부피와 균질 처리된 액의 부피가 거의 같도록 맞추었다. 이 폴리에틸렌 병을 밀 분산 장치인 페인트 쉐이커(paint shaker, 모델 PK2003T, PK Lab, 한국)에 장착하였다. 이 장치에는 분산액의 온도 상승을 막기 위해 냉각수 순환조로부터 5 ^oC의 냉각수가 흐르는 구리관으로 폴리에틸렌 병을 감싸도록 장치를 구성하였다. 페인트 쉐이커는 750 RPM에서 통상은 120분으로 운전되었으며 분산시간 테스트를 위해 30, 60, 90, 120분의 여러 시간 조건으로 운전되었다. 페인트 쉐이커의 분산을 거친 후 최종적으로 CNT 분산액을 확보하였다.
측정. 분산처리로 만들어진 CNT 분산액의 유변물성을 측정하기 위해 플레이트-플레이트 타입의 레오미터(모델 MCR-102, Anton Paar Co., Austria)를 사용하였다. 플레이트의 지름은 50 mm이고 플레이트간 간격은 1 mm로 설정되었다. 측정시 온도는 펠티어(Peltier) 소자 제어로 25 ^oC(± 0.1 ^oC)로 유지되었다. 선형 점탄성 거동과 정상 전단의 두 가지 측정 모드에서 측정이 이루어졌다. 선형 점탄성 모드에서는 각주파수 10 rad/s, 변형율 0.01-100% 범위에서 저장 및 손실 탄성률을 측정하였으며 정상 전단 모드에서는 1-1000 s^-1의 전단율 범위에서 측정이 이루어졌다. 전처리로서 측정 시료에 1분간 10 s^-1에서 전단을 가한 후 측정이 이루어졌다.
전기전도도 측정기(모델 HI 9733, 한나 계측기, 한국)를 사용해 CNT 분산액의 전기전도도를 측정하였다. 분산액 시료를 비전도성 플라스틱 용기에 넣고 측정기의 프로브(probe)를 시료에 잠기게 하여 전기전도도를 측정하였다.

입자 분산액 내 입자 응집은 유변학적 성질에 영향을 끼치는 데 입자의 응집이 진행되다가 응집체들이 연결되면서 네트워크 구조를 형성하면 그 영향은 더욱 두드러진다. 이 네트워크 구조를 퍼콜레이션(percolation) 혹은 콜로이드 젤(colloidal gel)이라고 부르는데 1 vol% 이하의 낮은 입자농도에도 잘 나타난다. 콜로이드 젤에서 응집체의 미시적 구조 변수와 탄성과 같은 거시적 물성의 비례적 관계로 표현하는 스케일링 이론으로는 Shih 등의⁵ 이론이 잘 알려져 있다. 고분자 젤에 대한 이론을 콜로이드 젤에 응용한 이들의 이론에 의하면 콜로이드 젤의 탄성이 콜로이드 젤을 구성하는 응집체 내부의 결합력에 주로 의존하는 강한 연결 영역(strong-link regime)과 응집체(floc)와 응집체간 결합력에 결정되는 약한 연결 영역(weak-link regime)으로 양분된다. 그러나 이 이론은 두 영역으로 뚜렷이 구분되는 경우에 적합하나 그렇지 않은 경우 비현실적인 결과를 보이는데 이를 극복하기 위해 Wu와 Morbidelli는⁶ Shih 등의 이론을 더 일반화하여 두 영역의 중간 영역을 고려한 아래의 식 (1)을 제시했다.



여기서 β=d-2+(x+2)(1-α)로 정의된다. 선형 점탄성 거동으로부터 구해지는 G'_lim와 γ_lim는 평탄(plateau) 영역 상단에서 저장 탄성률과 변형률이며 φ  는 CNT 입자의 부피분율이다. 기호 d는 유클리드 차원으로 3차원 공간에서 이 값은 3이 된다. 기호 d_f 는 응집체의 프랙탈 차원이고 x는 응집체 내부 중추의 프랙탈 차원이다. 그리고 α 는 강한 연결과 약한 연결 두 영역의 상대적 비중을 나타내는 매개변수로서 0에서 1 범위의 값을 가지는데 강한 연결 영역에서 0, 약한 연결 영역에서는 1이다.
식 (1)과 분산액의 농도에 따른 점탄성 변화를 이용하여 응집체의 프랙탈 차원을 구할 수 있다. 이를 본 연구의 CNT 분산액에 대해 적용한다. 분산시간을 2시간 거친 분산액 시료의 점탄성 거동을 CNT 입자의 농도별로 측정하여 그 결과를 Figure 2에 나타냈다. CNT 각 농도에 대해 변형률에 따른 저장 탄성률과 손실 탄성률의 변화로 나타냈는데, 낮은 변형률에서는 저장 탄성률이 일정한 평탄 영역을 보이고 변형률이 더 증가하면 평탄영역에서부터 저장 탄성률이 지속적으로 감소하는 반면, 손실 탄성률은 증가하는 양상을 보인다. 또한 CNT 농도 증가에 따라 저장 탄성률이 증가하는 전형적인 거동을 보인다.
식 (1)을 이용하기 위해서는 평탄 영역의 상단 즉 저장 탄성률이 평탄 영역에서 감소하기 시작하는 변곡점인 선형 한계 저장 탄성률과 변형률을 구해야 한다. Figure 2에서 저장 탄성률이 평탄 영역에서 미세하게 만곡의 형태를 띠어서 변곡점을 잡기가 용이하지 않음을 볼 수 있다. 따라서 체계적인 변곡점 설정이 필요한데 이를 위해 Carreau-Yasuda 모델을 회귀분석에 사용하였다.



여기서 γ , α, n은 회귀분석을 통해 결정되는 인자들이다. 선형 한계점은 식 (2)에서 변곡점 γ = 1/λ 위치에 해당된다. 식 (3)의 회귀분석 결과를 Figure 3에 나타냈는데 이 모델식이 평탄 영역과 변곡점 부근까지의 결과와 잘 맞아 이를 이용해 변곡점을 찾는 것이 적절함을 알 수 있다.
이렇게 결정된 G'_lim와 γ_lim를 각 CNT 농도별로 구하고 그 결과를 Figure 4에 나타냈다.
입자 농도 증가와 함께 G'_lim은 증가하고 γ_lim는 감소하는 형태로 나타나는 것을 알 수 있다. 통상 G'_lim은 농도에 따라 증가하므로 응집체의 성격은 γ_lim의 거동에 따라 결정된다. Figure 4의 형태는 응집체 내부의 응집력이 응집체와 응집체 사이의 응집력에 비해 더 큰 강한 연결 영역에 가까움을 보여준다. 이들 선형 한계 값들의 농도 의존성은 G'_lim∝φ^1.758로 각각 표현된다. 이를 식 (1)에 적용하면 프랙탈 차원 d_f 는 1.28, 매개변수 α는 0.33이 된다. 프랙탈 차원은 응집체 내 입자들의 밀집도와 형태를 나타내는데 1은 줄(string), 2는 면, 그리고 3은 구의 형태가 된다. 프랙탈 차원 1.28이라면 줄의 구조에 가까운데 섬유상 구조인 CNT의 경우 엉긴 형태보다는 풀어진 형태에 더 가깝다는 것을 의미한다. 그리고 α가 0.33이라는 것은 응집체 내부의 응집력(intrafloc link)이 응집체와 응집체간 응집력보다 우세한 강한 연결 영역이 67%, 약한 연결 영역이 33%로 분산액의 탄성에 기여하고 있다는 의미다.
저장 탄성률의 거동과 함께 응집체의 구조를 파악하는 데 잘 활용되는 유변학적 성질은 전단 항복응력(shear yield stress)이다. 프랙탈 응집체에 대한 질량-반경(mass-radius) 스케일링 관계와^2,3 응집체의 크기와 전단응력간 비례관계를 이용해 식 (3)과 같이 항복응력(t_y)과 입자 농도의 스케일링 식을 얻을 수 있다.^11-14



여기서 지수 m은 전단응력이 응집체 크기에 미치는 영향을 나타내는 척도이다. 식 (3)으로 지수 m을 결정하기 위해 전단응력 측정 결과로부터 항복응력을 구해야 한다. Figure 5(a)와 5(b)에 2시간 분산한 CNT 분산액의 농도별로 전단율에 따른 전단응력(t) 및 점도(h) 측정결과를 나타냈다.
이 결과에 대해 Hershel-Bulkley 모델을 적용하여 항복응력을 구하였다.



여기서 K와 n'은 각각 일관성과 흐름 지수들이다. Hershel-Bulkley 모델로 구한 항복응력을 Figure 6에 CNT 입자 농도별로 나타냈다.
이를 스케일링식으로 나타내면 τ_y∝φ^1.149이며 식 (4)와 앞에서 구한 프랙탈 차원 값을 이용하면 지수 m은 0.506이 된다.
이들 유변학적 성질과 함께 거시적 물성의 하나로 분산액의 전기전도도를 측정하였다. Figure 7에 2시간 분산한 CNT 분산액에서 CNT 입자 농도에 따른 전기전도도의 변화를 나타냈는데 입자의 농도에 따라 전기전도도가 거의 선형적으로 증가하는 경향을 보인다. 여기서 한 가지 주목할 점은 균질기만을 거친 분산액 상태, 즉 분산시간 0일 때 전기전도도가 거의 0으로 측정된다는 것이다. CNT 입자의 분산성이 매우 낮은 상태에서는 분산액 중 CNT의 전기 전도성 효과가 거의 나타나지 않는 것을 볼 수 있다.
이제 d_f, α, m 등의 응집구조 변수들이 분산시간에 따라 어떻게 달라지는지를 알아본다. 각 분산시간에서 이들 변수들을 구하기 위해 유변학적 물성을 측정하므로 우선 유변학적 물성의 변화를 살펴보았다. CNT 분산액의 각 농도에서 분산시간을 30, 60, 90, 120분으로 변화시켜 가면서 각 농도에 대해 변형률에 따른 저장 탄성률과 전단율에 따른 점도 변화를 측정하였다. 그 대표적인 결과를 Figure 8과 Figure 9에 나타냈다. 입자농도 0.37%와 0.56%의 결과인데 Figure 8(a)와 8(b)에서 보듯이 각 농도에서 분산시간에 따라 저장 탄성률이 약간씩 증가하였다. 그리고 입자 농도가 낮을수록 분산시간에 따른 저장 탄성률의 증가가 상대적으로 더 크게 나타나다가 입자 농도가 증가하면서 점진적으로 그 증가폭이 줄어들었다. Figure 9의 점도 결과도 비슷한 양상을 보이는데 이를 좀 더 잘 표현한 것이 Figure 10과 Figure 11이다.
Figure 10은 각 농도에서 실측 편차가 없는 1.1% 변형률에서 저장 탄성률 값을 나타냈는데 분산시간에 따라 약간씩 증가하고 입자의 농도가 증가하면서 그 증가 폭이 줄어드는 것을 볼 수 있다. Figure 11의 점도 결과도 유사하게 나타났다. 이는 초기에 큰 응집체를 형성하다가 분산이 진행되면서 응집체가 작아지게 되는데, CNT의 섬유상 구조의 특성상 여러 섬유상의 CNT가 엉겨 덩어리진 상태에 있다가 분산이 이루어지면서 엉긴 구조가 풀어져 가늘고 광범위한 네트워크 형태가 형성되어 나타난 결과로 해석된다. 이와 유사한 결과는 Kim과 Choi의¹⁰ 최근 연구에서도 볼 수 있다. MW-CNT와 n-methyl-2-pyrrolidone 그리고 nitrile butadiene rubber 계통의 분산제로 구성된 분산계에 대해 분산시간에 따른 유변학적 물성과 전기전도도 변화를 제시했는데 1시간까지 점도나 저장 탄성률, 그리고 전기 전도도가 모두 증가하는 것을 볼 수 있다. 본 연구에서도 분산시간에 따른 전기전도도의 거동을 확인할 수 있는데 Figure 12에 나타낸 각 입자농도에서 분산시간에 따른 전기전도도의 변화를 보면 전체적으로 분산시간에 따라 전기전도도가 증가하는 것을 알 수 있다.
그리고 전기전도도의 증가폭이 분산시간 60분 이상이나 입자 농도가 높은 경우 크게 감소하여 전기전도도가 일정하게 되는 거동도 Figure 10과 Figure 11의 유변학적 거동과 유사하다. 전체적으로 보면 분산시간에 따라 전기전도도는 증가하고 있어 엉겨 있던 CNT 응집체가 풀어져 가늘어지면서 광범위해 진다는 해석에 부합된다고 하겠다. 참고적으로 분산시간이 지나치게 길어지면 파쇄되는 CNT 입자들이 증가할 수 있어¹⁵ 정확한 해석이 어려워질 수 있다. 이런 점에서도 본 연구는 분산 시간의 최적화가 아니라 분산시간에 따른 응집구조 변화를 정량적으로 알아보는데 초점을 맞추었다.
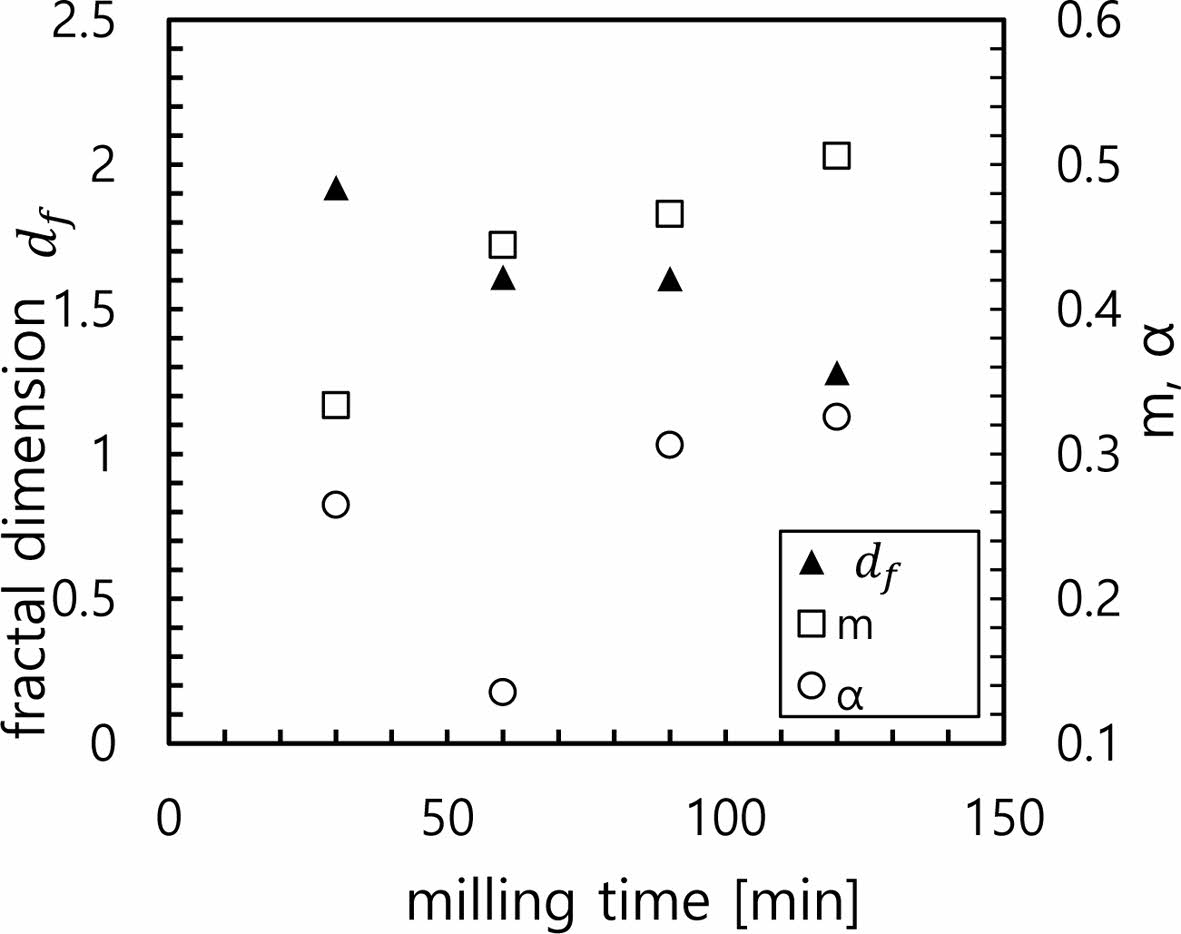
앞에서 설명한 바와 같이 각 분산시간별 입자농도별 측정한 유변학적 물성을 스케일링 이론에 적용하여 응집 구조 변수들을 구하였다. Figure 13에 분산시간에 따른 이들 응집 구조 변수들을 나타냈다.
분산시간이 증가하면서 프랙탈 차원은 분산시간 30분에서 1.92에서 분산시간 120분에서 1.28로 지속적으로 감소하였다. 프랙탈 차원으로 구분되는 전형적인 응집 형태는 빠른 응집과 줄 모양의 속성을 띠는 diffusion limited cluster aggregation (DLCA)와 상대적으로 느린 응집과 입체적 모양을 특징으로 하는 reaction-limited cluster aggregation(RLCA)이다. DLCA는 입자간 접촉이 일어나면 응집되는 형태로 프랙탈 차원 값은 약 1.7-1.8의 값을 가지고 입자간 접촉이 일어나도 응집이 일어날 확률이 상대적으로 낮은 RLCA의 경우 약 2.1-2.2 정도의 값을 가진다. 분산시간 30분에서는 RLCA와 DLCA의 중간 정도의 값인 1.92에서 분산시간이 증가하면서 점점 감소해서 120분에서는 1.28 정도의 낮은 값을 가진다는 것은 응집체가 2차원적인 면 형태에서 1차원적 선 형태로 변해가는 것을 의미한다. 이 프랙탈 차원의 변화는 분산이 진행되면서 응집체의 구조가 변하는 것을 뚜렷이 보여주는 결과라 하겠다. 선행 연구 결과를 보면 MW-CNT(평균길이 10 mm, 직경 대 길이비 약 200)와 저분자 폴리이소부틸렌(polyiso- butylene) 분산계에서는¹⁶ 프랙탈 차원이 2.45, MW-CNT(길이 0.1-2.2 mm, 직경대 길이비 45)와 에폭시 수지 분산계에서는⁷ 2.15, MW-CNT와 불포화 폴리에스터 수지용액 분산계의⁸ 경우 1.28로 나타났다. 특히 불포화 폴리에스터를 사용한 경우는 분산을 위해 MW-CNT의 표면을 리튬(lithium)과 스티렌(styrene)으로 처리한 것이다. 별도의 표면처리를 하지 않은 MW-CNT를 사용한 경우 프랙탈 차원이 2.45와 2.15로 상대적으로 높은 반면 분산성을 좋게 하기 위해 MW-CNT의 표면처리를 한 것은 뚜렷이 낮은 1.28의 프랙탈 차원을 보인 것이다. 본 연구에서도 CNT의 분산성을 위해 고분자 분산제(트윈 80)를 사용하고 있어 프랙탈 차원이 1.28로 나온 Urena-Bidevades 등의⁸ 결과와 같은 수치로 보인 것으로 생각된다. 실제 트윈 80은 응집체의 침강이 없이 균질하고 안정된 CNT 분산액을 형성하는 데 매우 중요한 역할을 하는 것으로 실험적으로 관찰되었다.
다음으로 α의 변화를 보면 분산시간 60분에서 다소 감소하나 전체적으로 분산시간에 따라 약간씩 증가하는 형태로 나타난다. 즉 응집체 내 입자들간 응집력이 응집체와 응집체간 응집력보다 상대적으로 더 큰 강한 연결 영역의 비중이 감소하고 약한 연결 영역의 비중이 늘어나는 것을 의미한다. 앞서 언급한 선행 연구 결과에서도^7,8 α는 0.35-0.41의 범위에 있다.
지수 m의 경우 분산시간 증가와 함께 0.33에서 0.51로 증가한다. 지수 m에 대해서도 많은 선행 연구 결과들이 있는 데 Potanin은¹⁵ 이론적 계산을 통해 입자와 인접 입자사이의 상호작용이 입자의 중심과 중심사이 거리만 고려하는 연응집체(soft aggregates)의 경우 m이 약 0.4-0.5이고 인접 입자 간의 상호 작용이 중심과 중심간 거리 뿐만 아니라 비중심(non-central)적인 상호작용까지 포함하는 경응집체(rigid aggregates)의 경우 m이 0.23-0.29임을 보였다. 그러나 이들 값들이 엄격히 적용되는 것은 아니며 실제 분산계는 이들 두 수치 범위의 중간 영역에 존재하는 경우가 많다. Sonntag과 Russel은¹⁷ 폴리스티렌 입자와 글리세롤 분산계에서 m이 0.35인 측정 결과를 얻었으며 Eggersdorfer 등은¹⁸ 연응집체 분산계에 대해 m이 0.35-0.37이라는 계산 결과를 얻었다. 따라서 m의 절대값보다 이 값의 변화 양상을 보는 것이 중요하다.
분산시간에 따라 지수 m이 0.33에서 0.51로 증가한다는 것은 입자들이 엉겨 있는 경응집 상태에서 분산이 어느 정도 이루어지면서 연응집 상태로 변해가는 결과로 해석된다. CNT 분산계에 대한 선행 연구 결과를 보면 0.32, 0.34의^7,8 m값을 보였는데 이는 식 (3)이 아닌 Potanin이 제시한 근사식을 이용한 것이다. 경응집체로 가정할 경우 이 근사식에서 m은 간단히 1/β와 같다. 여기서 β는 식 (1)에서 정의되는 매개변수로 프랙탈 차원과 함께 결정된다. 이러한 방법을 본 연구 결과에 적용하면 m은 0.28-0.33의 범위의 값을 가져 선행 연구 결과들과 비슷한 값을 가짐을 알 수 있다. 식 (3)으로 구한 m값의 변화에 비해서는 작으나 분산시간에 따라 전체적으로 약간 증가한다. 전체적으로 보면 분산이 진행되면서 프랙탈 차원은 뚜렷이 감소하고 α와 m은 증가한다.

고분자 분산제와 혼합된 에틸렌글리콜에 분산된 MW-CNT 입자의 응집 정도를 프랙탈 개념에 기초한 스케일링 이론^5,6,11-13을 이용하여 정량적으로 분석하였다. CNT 분산액의 저장 탄성률과 항복응력 등의 탄성적 성질의 농도 의존성으로 표현되는 스케일링 이론을 적용하여 응집체의 미시적 구조 변수인 프랙탈 차원, 응집체 내부와 응집체간 응집력의 상대적 크기를 나타내는 구조 매개변수 α, 전단력에 의한 응집체 크기 변화를 나타내는 지수 m등의 미시적 구조 변수들을 구하였다. CNT 분산액의 분산 상태에 따른 이들 응집 구조 변수들의 변화를 알기 위해 분산시간을 30, 60, 90, 120분으로 변화시켜 가면서 유변학적 물성을 측정하였다. 분산시간의 증가에 따라 저장 탄성률과 점도는 전체적으로 증가하는 경향을 보였는데 CNT 입자의 농도가 높거나 분산시간이 커질수록 저장 탄성률이나 점도의 증가 폭이 감소하였다. CNT 분산액의 전기전도도도 이러한 유변학적 물성의 변화 경향과 대체로 유사하게 나타났다.
미시적 구조 변수들의 변화는 분산시간 증가에 따라 프랙탈 차원이 1.92에서 1.28까지 뚜렷이 감소하는 경향을 보이며 매개변수 α와 지수 m은 증가하는 경향을 나타냈다. 프랙탈 차원의 변화를 통해 분산이 진행되면서 CNT 입자들이 엉겨 있는 2차원 구조에서 1차원 구조로 변화해가는 것을 확인할 수 있었다. 분산시간 증가에 따라 매개변수 α는 응집체 내부보다는 응집체간 응집력이 상대적으로 약간 더 증가하는 경향을 띠고 지수 m도 증가하는 경향으로 나타나 경응집체 상태에서 연응집체 상태로 변해가는 것을 보여준다. 이러한 매개변수 α와 지수 m의 변화는 프랙탈 차원으로 나타난 엉킨 구조에서 선형적 구조로 가면서 나타날 수 있는 변화로 해석된다.
전체적으로 CNT 분산액의 탄성적 성질에 대한 스케일링 이론을 이용한 응집 구조 해석이 매우 유의미한 결과를 제공함을 확인하였다.