- Study and Design of High Strength and Low Heat Generation Polymer Composites by Molecular Dynamics Simulation
College of Chemistry & Chemical Engineering, Institute of High Performance Rubber Materials & Products, and Key Laboratory of Environment-Friendly Polymeric Materials of Anhui Province, Anhui University, Hefei 230601, China
- 분자동역학 모사를 이용한 고강도, 저발열 고분자 복합재료 설계 및 연구
The molecular dynamics
simulation was used to study and design a polymer composites system with
excellent mechanical strength and less heat generation in a dynamic process. A
series of system factors such as filler loading, surface modification onto
filler, and network of cross-linking filler particles on mechanical and heat
generation of polymer composites are systematically considered. It is found that the surface
grafting onto fillers can restrain the heat generation of polymer composite in
the dynamic process, while it shows less effect on the mechanical property. A
network of cross-linking filler particles can be fabricated by a combination of
grafting chains onto fillers. By filling such a network into the polymer, the
mechanical and heat generation properties of polymer composites are
significantly improved. Simulation results can help experimental fabrication of
polymer composites with excellent mechanical and heat generation properties.
A network of cross-linking filler particles is
theoretically designed by combining ends of grafting chains onto fillers.
Molecular simulation study shows that the mechanical and heat generation
properties of polymer composites are significantly improved by filling such
network into polymer. Simulation study explored a potential way to fabricate
strong and low heat generation rubber materials.
Keywords: molecular dynamics simulation, polymer composite, surface modification, cross-linking network
The authors acknowledge the support
from National Key R&D Program of China (No. 2017YFB
0406204), National Natural Science Foundation of China (No.
51973002) and University Institution of High Performance
Rubber Materials of Anhui Province.
Inorganic fillers are important to physical properties of polymer
composites, such as carbon blacks are added into rubber to enhance the
mechanical properties of rubber products.1-3 However, for elastomer
materials those undergo high-frequency dynamic repeating deformation, inorganic
fillers may increase the heat generation in dynamic process owing to the
friction between fillers and polymers.4 Such as, Kucherskii and
collaborators found that the rubber composites with carbon black as fillers
show stronger rigidity during the stretching process, and increased heat
generation during the relative sliding process.5 As is well known,
heat flux will damage the mechanical and aging properties of polymer materials.
Surface modification on fillers may be an effective way to restrain heat
generation in polymer composites. Theoretically, people predicted that surface
treatment onto fillers will improve the dispersion of filler particles in
composites.6 Obviously, surface modification may improve affinity
between fillers and polymers and so make a good dispersion of fillers in
composites, which will reduce the friction between fillers. Liu and
collaborators carried out molecular dynamics simulations on polymer composites,
they found that surface grafting onto nanoparticles can improve its dispersion,
with the increasing of grafting density and length, the Payne effect reduces
accordingly.7 Researchers have developed many experimental
technologies to surface modify filler particles, such as, surface grafting
polymer chains,8,9 plasma treatment,10-12 in situ
modification and sol-gel method etc.13-16
These surface modifications onto fillers improved tensile strength and
elongation at break of polymer composite. However, previous researching reports
less data on heat generation of polymer composites in the dynamic process. It
is hard to determine the effect of surface modification on heat generation of
polymer composites.
In this theoretic study, we carried out molecular dynamic simulation on
polymer composites. By constructing cross-linking polymer models and surface
modified filler particles, we studied the effect of surface modification on
mechanical property of polymer composites and heat generation during dynamic
process. To make polymer composites with strong mechanical strength and less
heat generation we built a cross-linking network of modified fillers and make
such network penetrate into the network of polymer chains. Our simulation
results are illuminating to experimental researching.
We performed classical molecular dynamics simulation methods to study the
polymer composites. The polymer chain is represented by a bead spring model
developed by Kremer and Grest,17 individual beads are connected by a
finite expandable nonlinear elastic (FENE) potential.18 Interaction
between nonbonding beads are represented by expended Lennard-Jones potential.
To distinguish coarse-grained beads of filler and polymer segment, we set the
diameter of polymer and grafted chain beads are s and mass of them
to be m respectively, while the diameter and mass of filler beads are 4s and 64m respectively. Due to the dimensionless
units setting, m and s are 1 in the
simulation. Liu et al. once performed molecular dynamic simulation on
polymer composites, and their simulation results are reasonable and accordant
to experimental observation. In this study, we set up the parameters which are
the same in reference.19 We constructed a three-dimensional polymer
network and each lattice of the polymer network is composed of 10 polymer
beads. The cross-linking degree of such network is calculated as number of
cross-linking beads over number of polymer beads, which is 6.43% for all
composites. Filler particles are imposed into the polymer networks. Filling
degree represented by n is defined as n=N/M, where N
is the total number of filler beads and M is the total number of polymer
beads, keep the number of filler beads and polymer beads unchanged to make the
filling degree equal in different systems. We considered three kinds of filler
particles in the simulation as shown in Scheme 1, those are (a) native particle
(nP) without surface modification; (b) surface grafted particle (gP) whose
surface is grafted with polymer beads; (c) a network of particles (cP) by
cross-linking grafting chain at surfaces of adjacent particles.
NPT ensemble and periodic boundaries were employed in simulation. The
simulated temperature is fixed at T*=1.0 and the pressure is fixed at P*=0
through the Nose-Hoover hot bath. The system are fully equilibrated (more than
107 cycles). The model was equilibrated and then stretched at strain ratio
of 327% (εmax=3.27) at NVT ensemble to get stress-strain
curves of polymer composites. The stress σ is calculated as the same with that
in reference.19 To calculate heat generation of polymer
composites during cyclic deformation, we imposed cyclically tensile loading
processes at strain ratio of 20% (εmax=0.2) for equilibrated
composites, which will produce a hysteresis loop of loading and unloading
stress-strain curves. The area of hysteresis loop of stress-strain curves is
calculated to represent the energy loss during dynamic process, which will be
released in the form of heat in the experiment and correspond to the heat
generation of polymer composites during dynamic process. More simulation
details are consistent with those in reference.19 The simulation
process was implemented using a large-scale atom/molecule integrated parallel
simulator (LAMMPS) developed by Sandia National Laboratory.20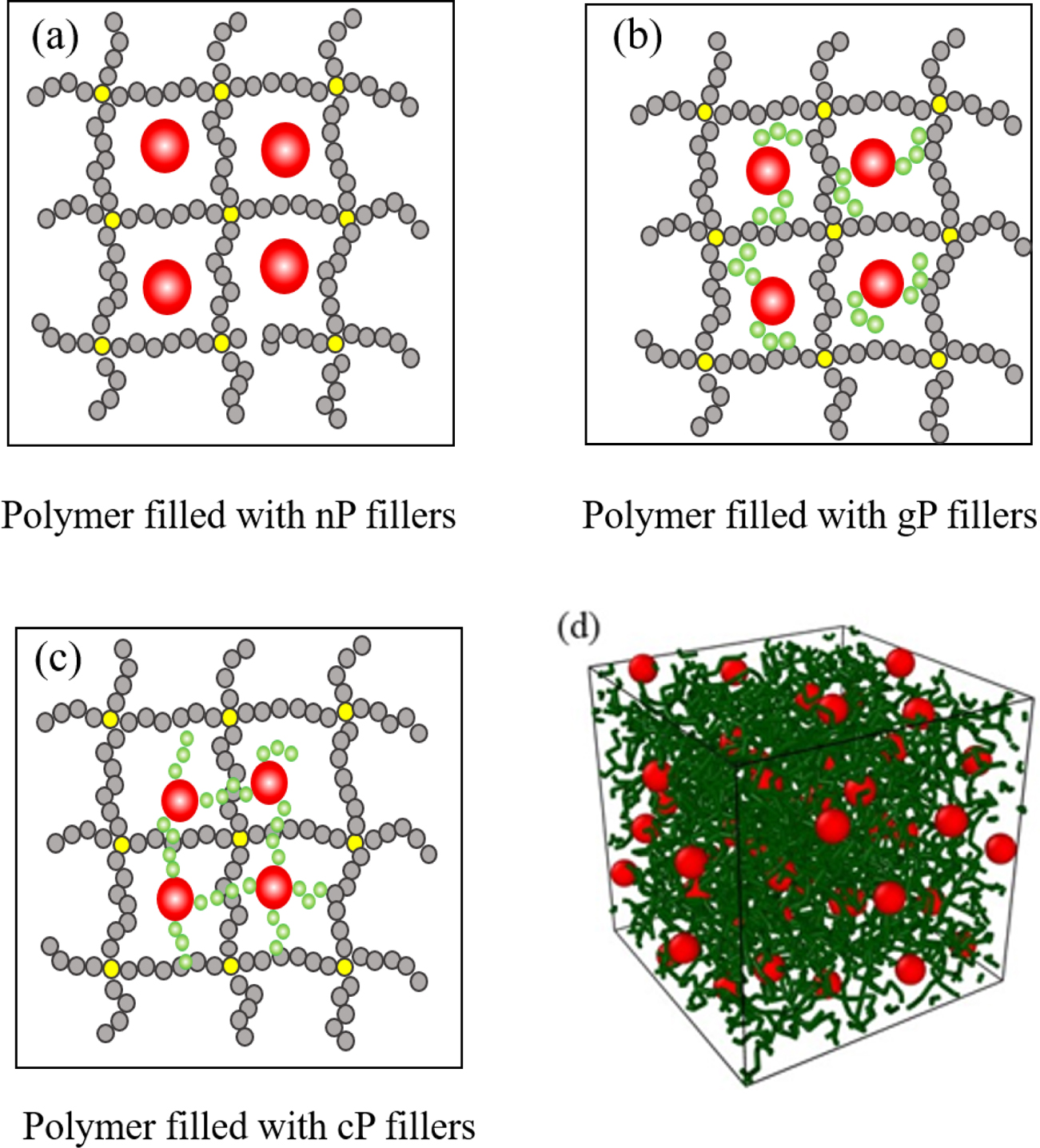
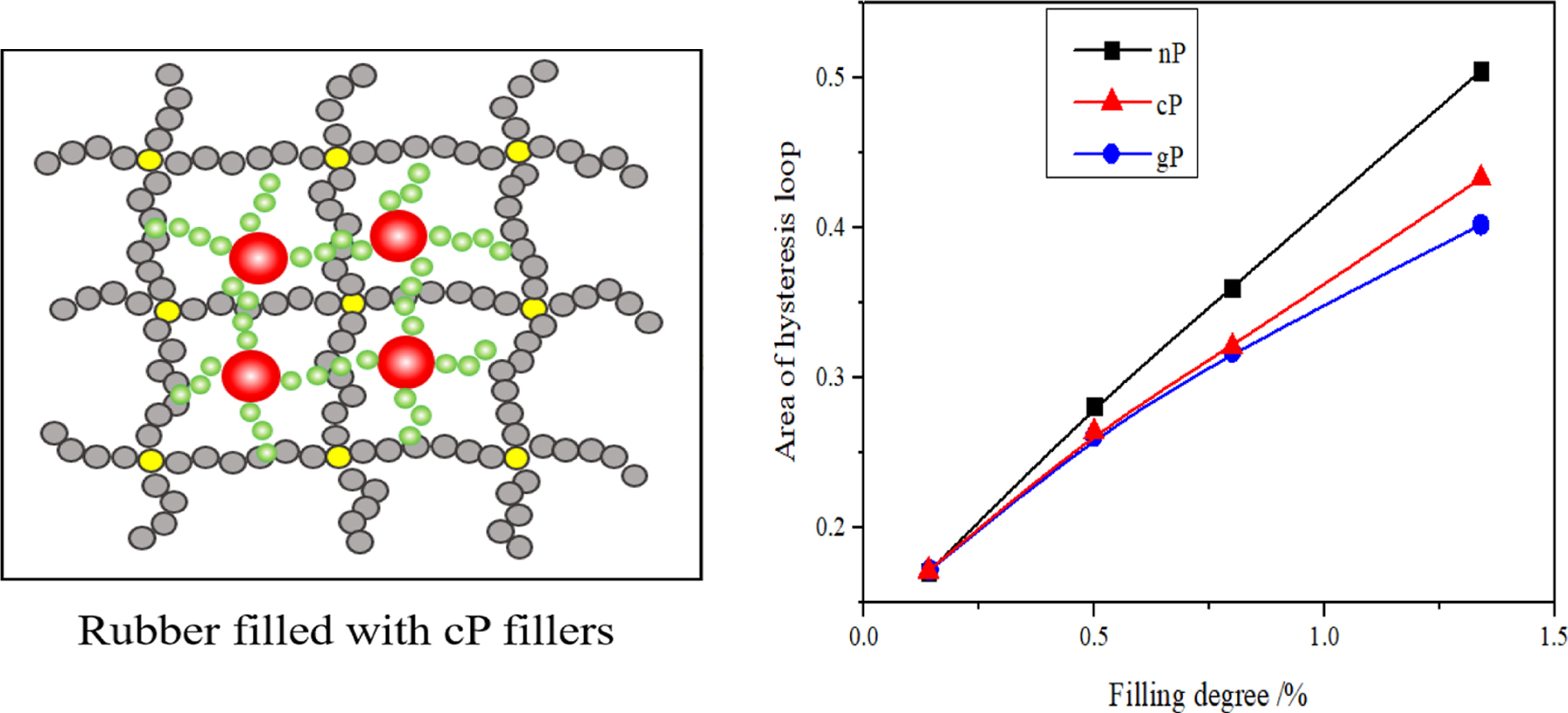
Scheme 1. Simulation models of polymer composites: (a) polymer
filled with nP fillers; (b) polymer filled with gP fillers; (c) polymer
filled with cP fillers; (d) a typical snapshot of filled polymer composites.
Effect
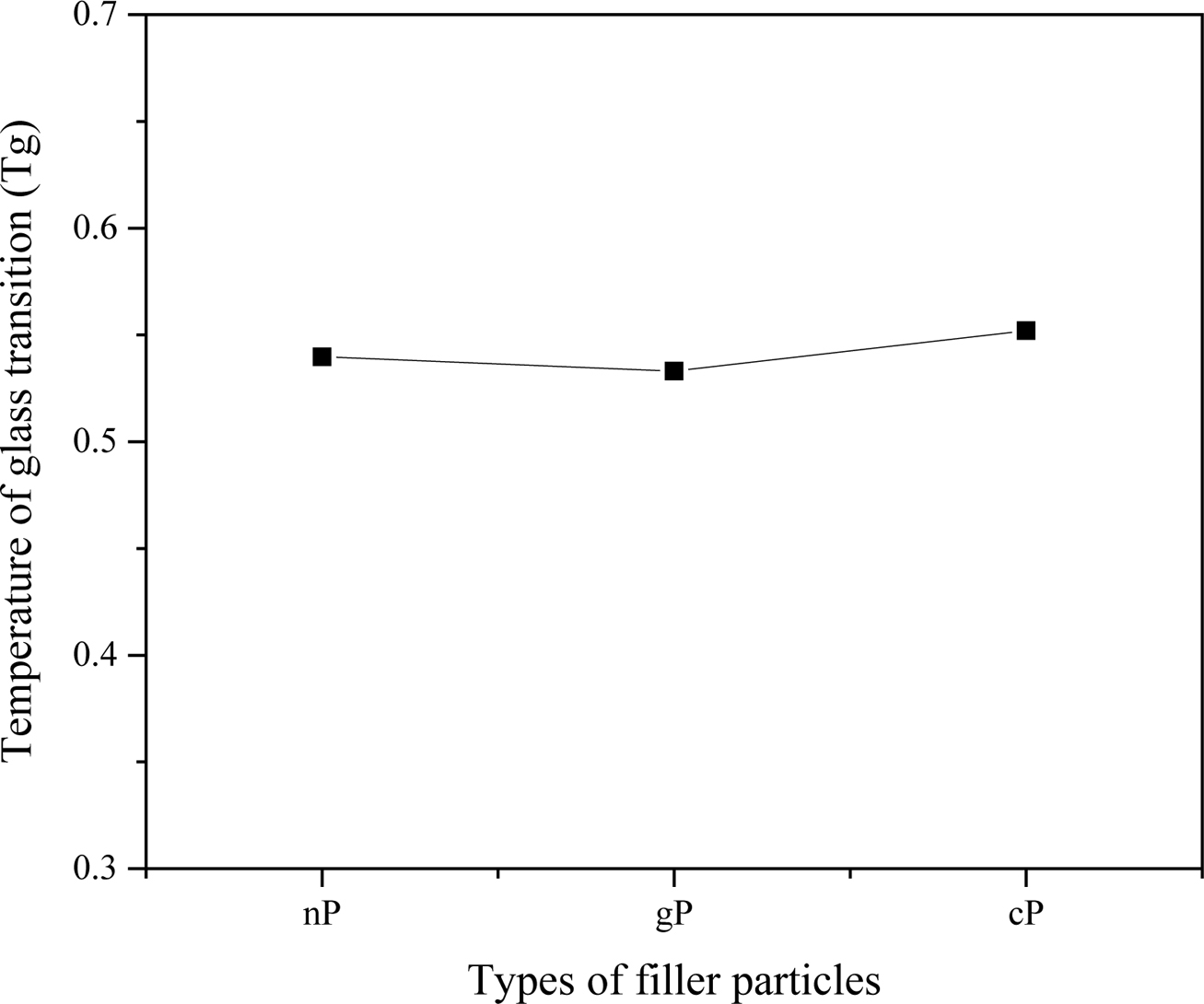
of Filling on Temperature of Glass Transition (Tg) of Composite Materials. To simulate a
polymer composite, system temperature must be higher than Tg
of polymer composites. We equilibrate composites model with a cooling rate of
5×10-4/t to gradually
decrease temperature recording the variation of composites density. The Tg
value of composites is estimated from the break point of linear variation of
composites’ density. For polymer composites filled with three kinds of filler
particles (nP, gP and cP, respectively), the Tg values of
them are about 0.55, as shown in Figure 1. In the following simulation, we set
the system temperature at 1 to ensure the system being a rubber state.
Effect
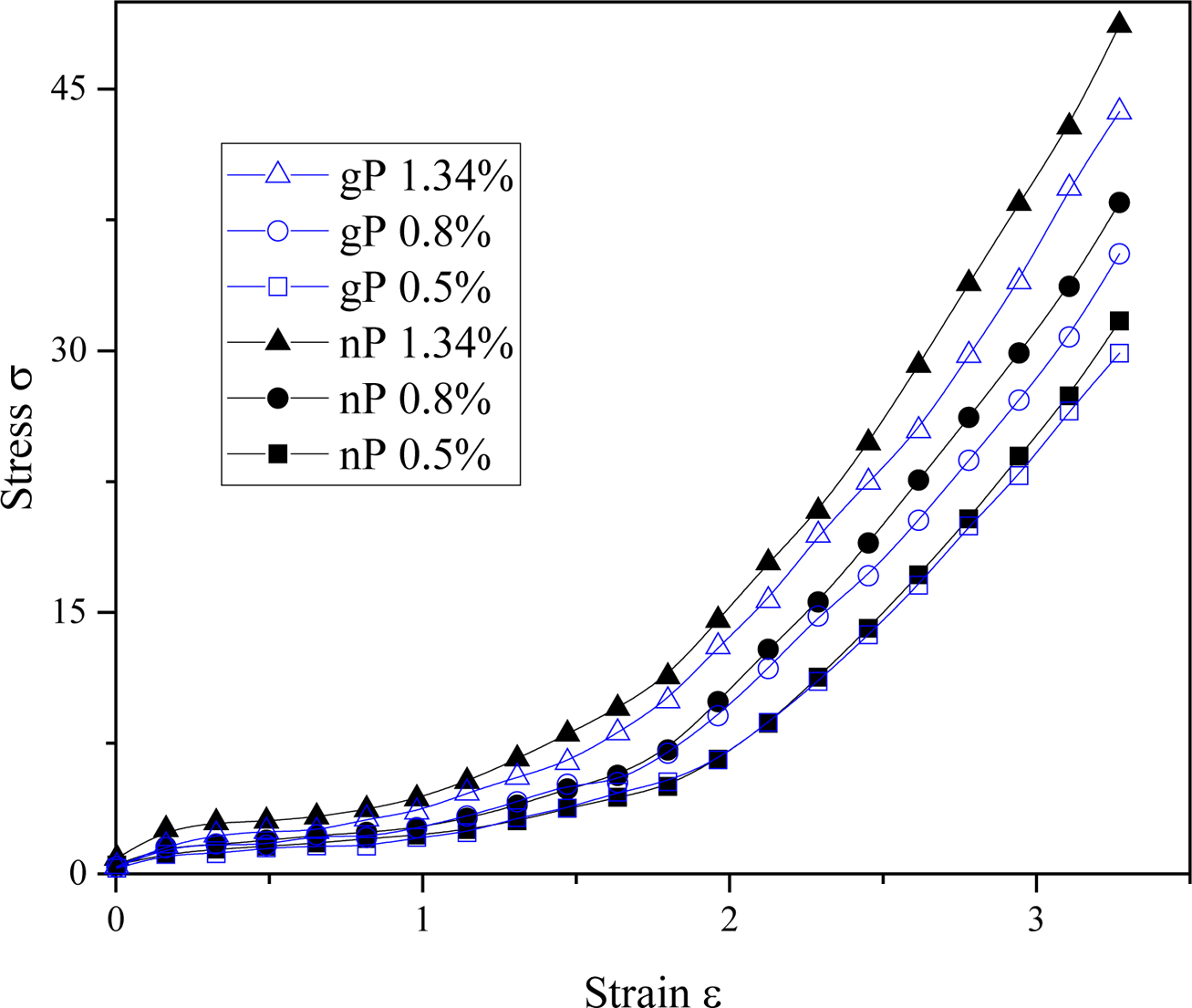
of Filler Loading on Mechanical and Heat Generation of Polymer Composites. Firstly, we
compared the effect of different fillers on mechanical and heat generation of
polymer composites. We imposed three types of fillers with the same filling
degree into a cross-linked polymer matrix respectively. For grafted particles
(gP), there are six chain segments symmetrically grafted onto the surface of a
native particle, each chain segment is composed of three beads. Grafting chain
segments between the nearest adjacent gP are furtherly combined to form a
cross-linked particles (cP) network involved in the polymer network. As shown
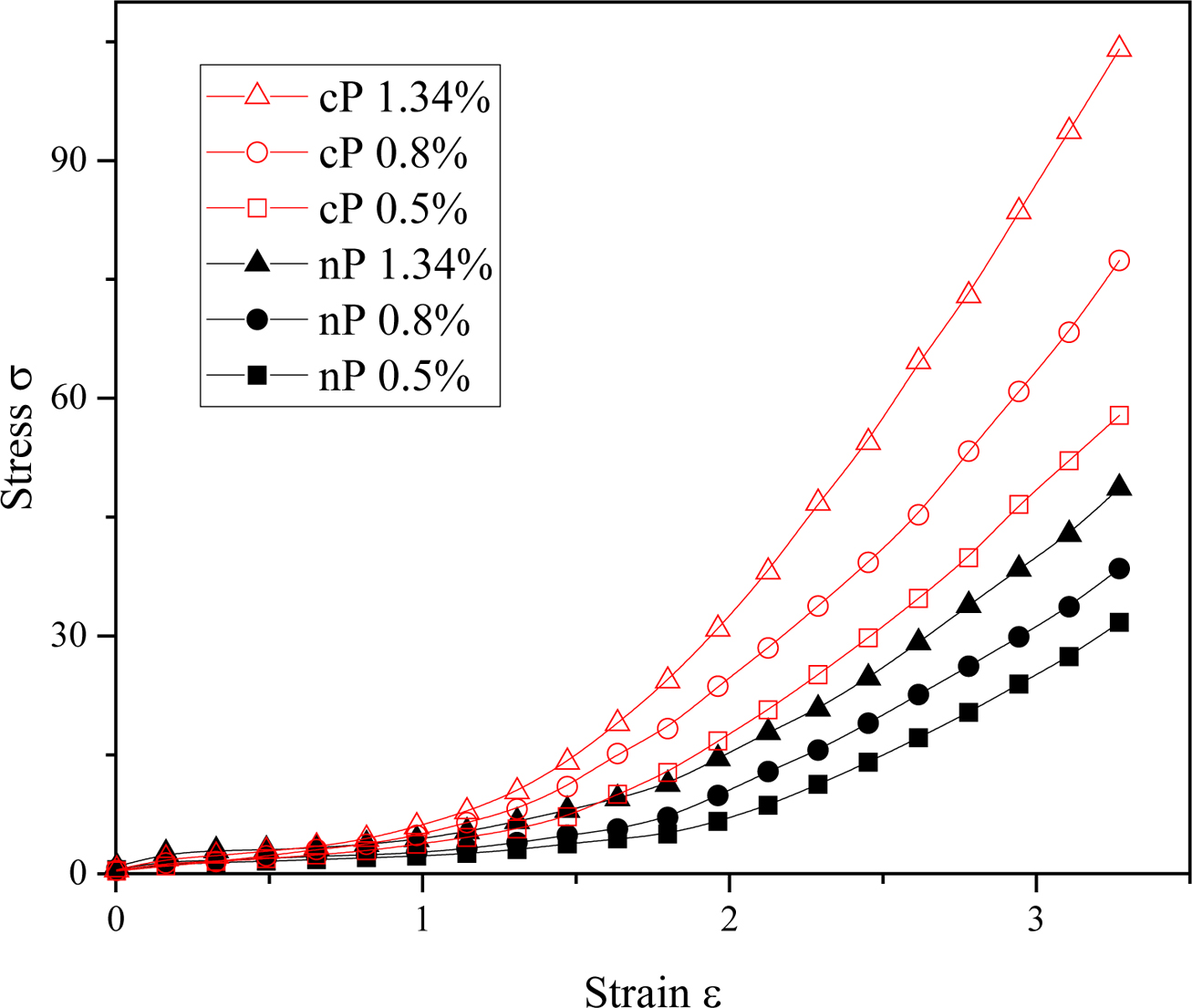
in Figure 2 and 3, the mechanical strength of all polymer composites are
improved correspondingly by filling degree increasing from 0.5% to 1.34%. In
Figure 2, the mechanical strength of polymer composites filled with grafted
particles (gP) are slightly less than those filled with native particles (nP).
This is because in our simulation model grafting of polymer beads decreases
filling content of composites in somewhat. It is worth to be noted that, in
Figure 3 polymer composites filled with cP network exhibit excellent mechanical
strength than those filled with nP. This means, the network of cP may
effectively strengthen the polymer matrix in comparison with gP does. The same
as in reference,19 the mechanic strength of polymer composites are
enhanced with the increase of fillers.
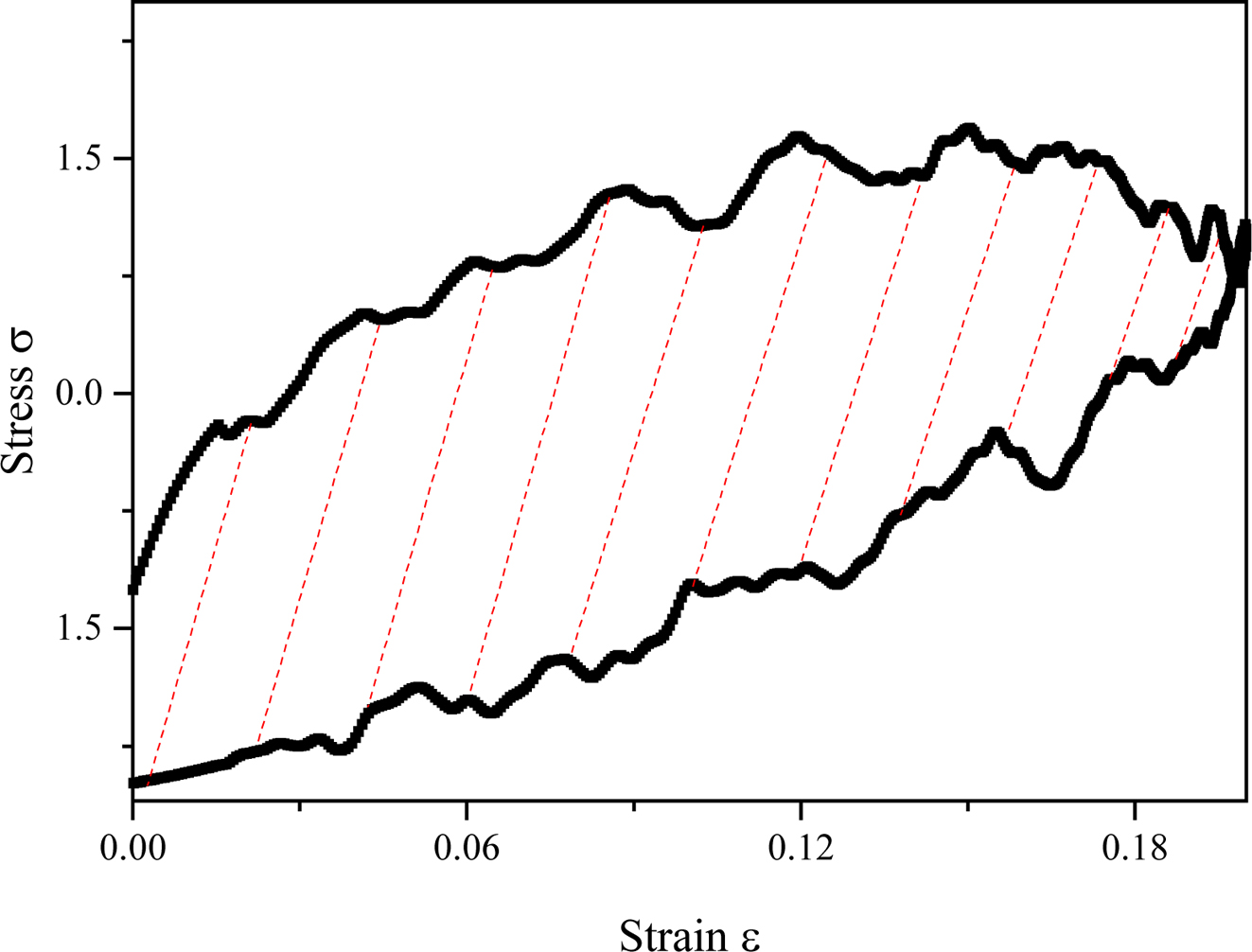
To study the effect of filler loading on heat generation, we calculated
the area of a hysteresis loop of loading and unloading stress-strain curves as
shown in Figure 4. To avoid the random error, the area values are averaged with
at least 19 hysteresis loops of loading and unloading stress-strain curves,
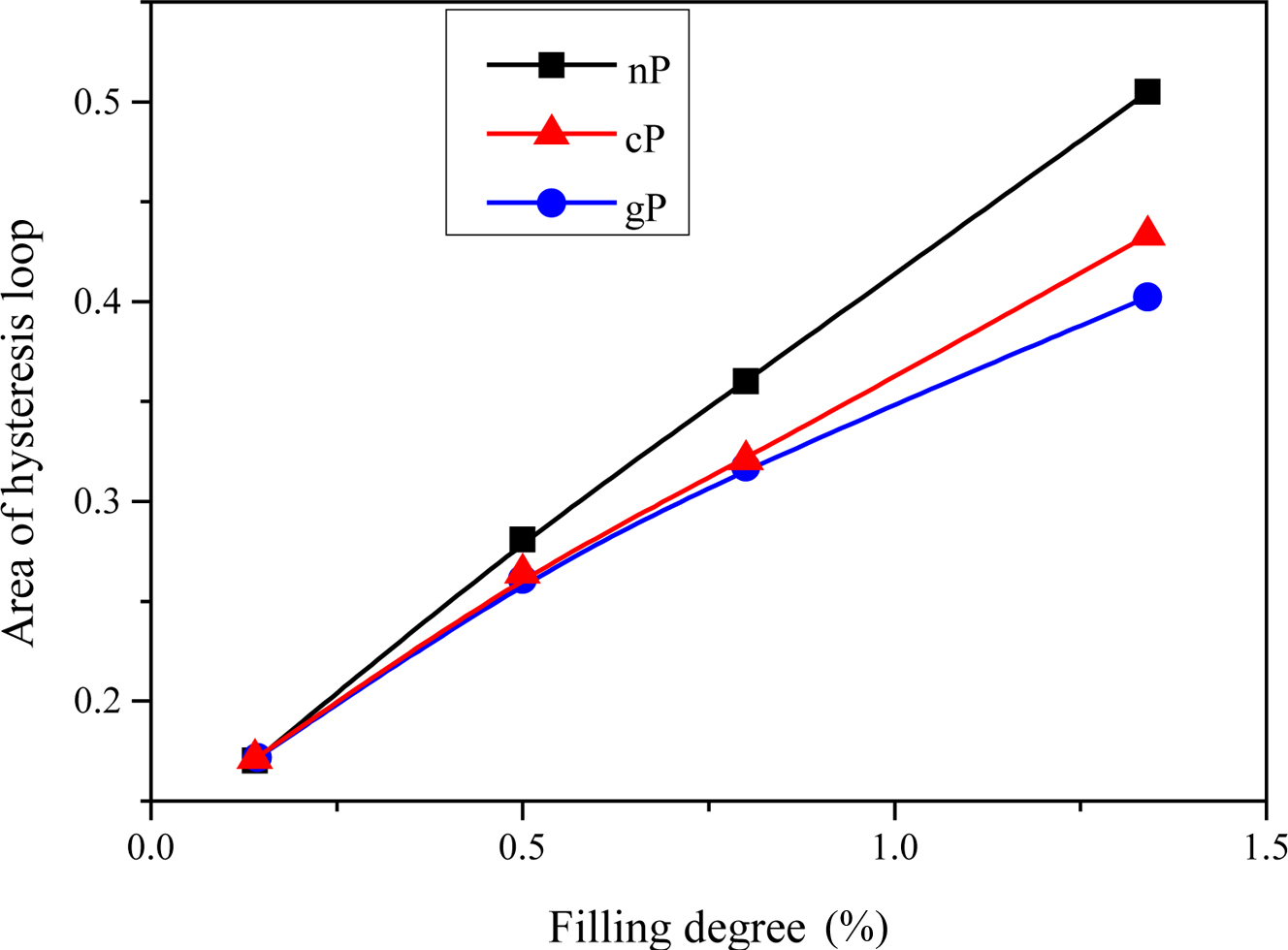
those are shown in Figure 5. It is obviously, the area values increase along
with increasing of filling degree for all polymer composites, while those of
polymer composites filled with gP and cP are lower than that filled with nP.
This means surface grafting may effectively decrease heat generation of polymer
composites during dynamic process. Considering the excellent mechanical
strength of polymer composites filled with cP network as shown in Figure 3, it
is worthy to study the effect of cP network on mechanical and heat generation
properties in deep.
Effect of cP Network on Mechanical and Heat Generation Properties of Polymer Composites.
As discussed above, the cP network may effectively strengthen polymer
composites, at the same time restrain the heat generation during dynamic
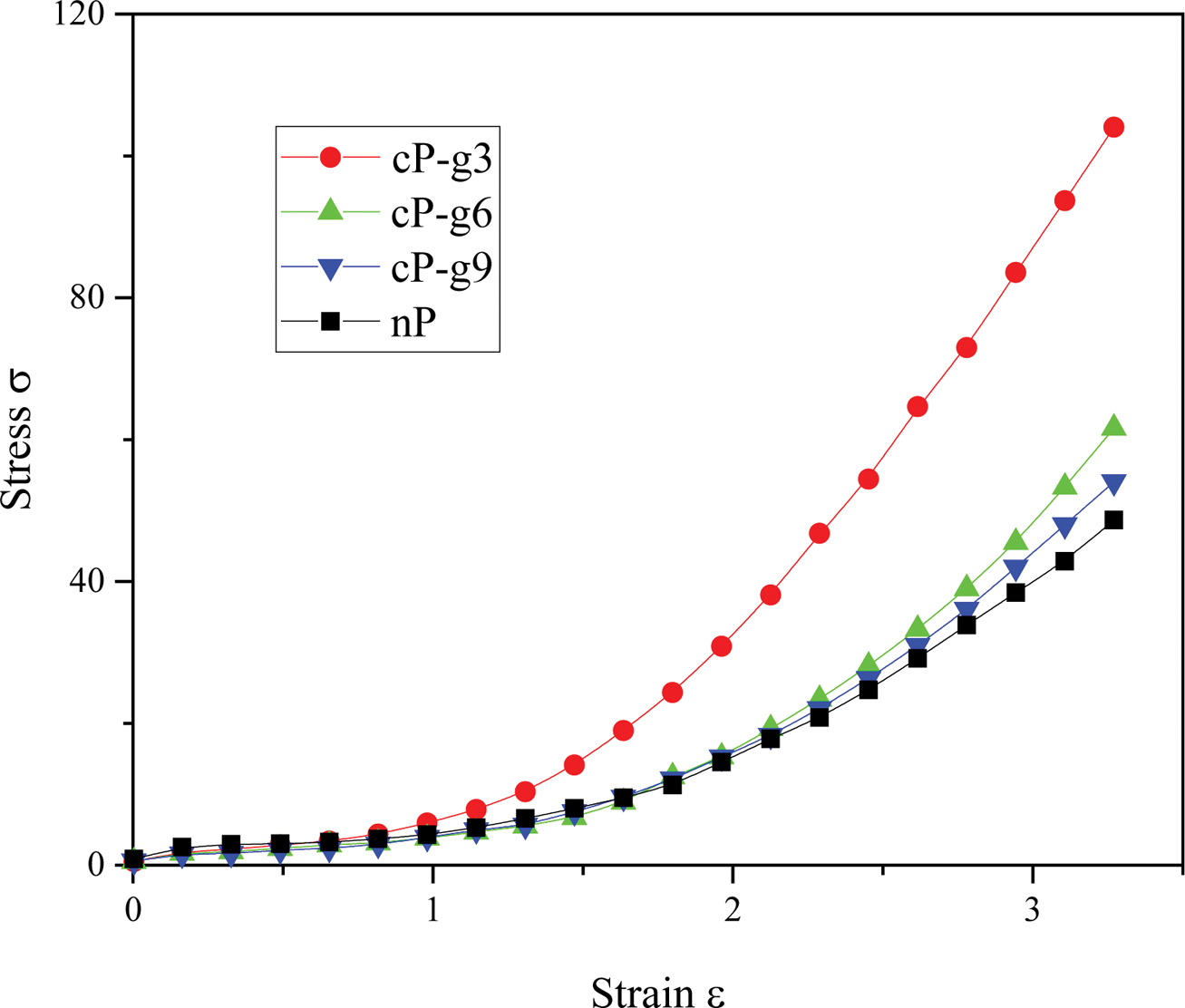
process. We considered different grafting chain length in cP network to find
out the reason of network structure on affecting mechanical and heat generation
properties. Grafting chain lengths onto the particle surfaces are varied from 3
beads to 9 beads. The stress-strain curves can be found in Figure 6. With
increasing of grafting chain lengths, the strength of polymer composites
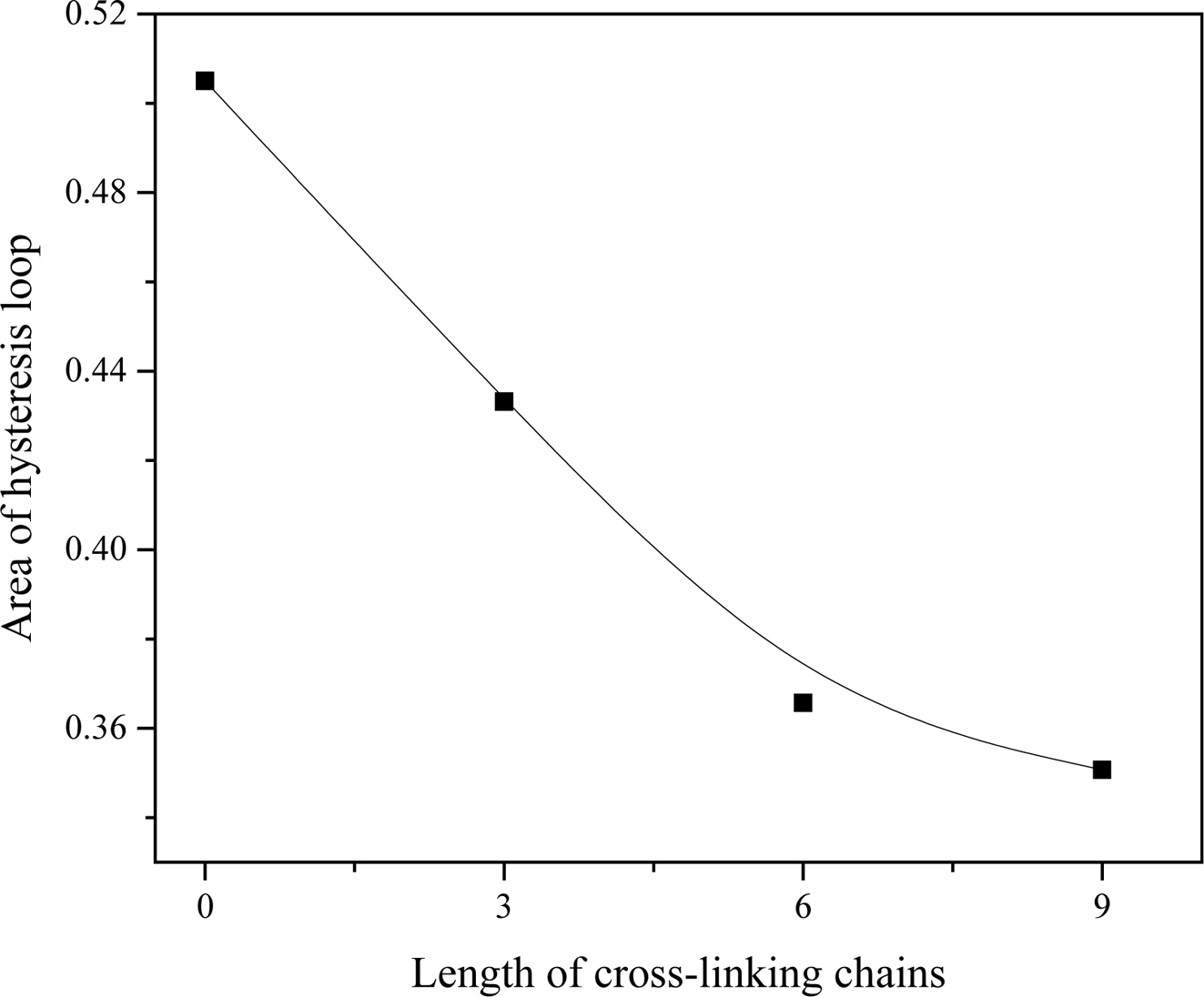
reduces rapidly. In Figure 7 the area of the hysteresis loop of stress-strain
curves of polymer composites reduced along with the increasing of grafting
chain lengths. We think this is because surface grafting chains covered the
particles from each other, and so reduced the interaction between filler
particles. As a result, the filler particles interact predominantly with
polymer chains, which reduce the heat generation from friction of fillers as
shown in Figure 6. In cases the grafting chain length is rather short, such as
3 beads in Figure 6, the network of cP is rather intensive, which can
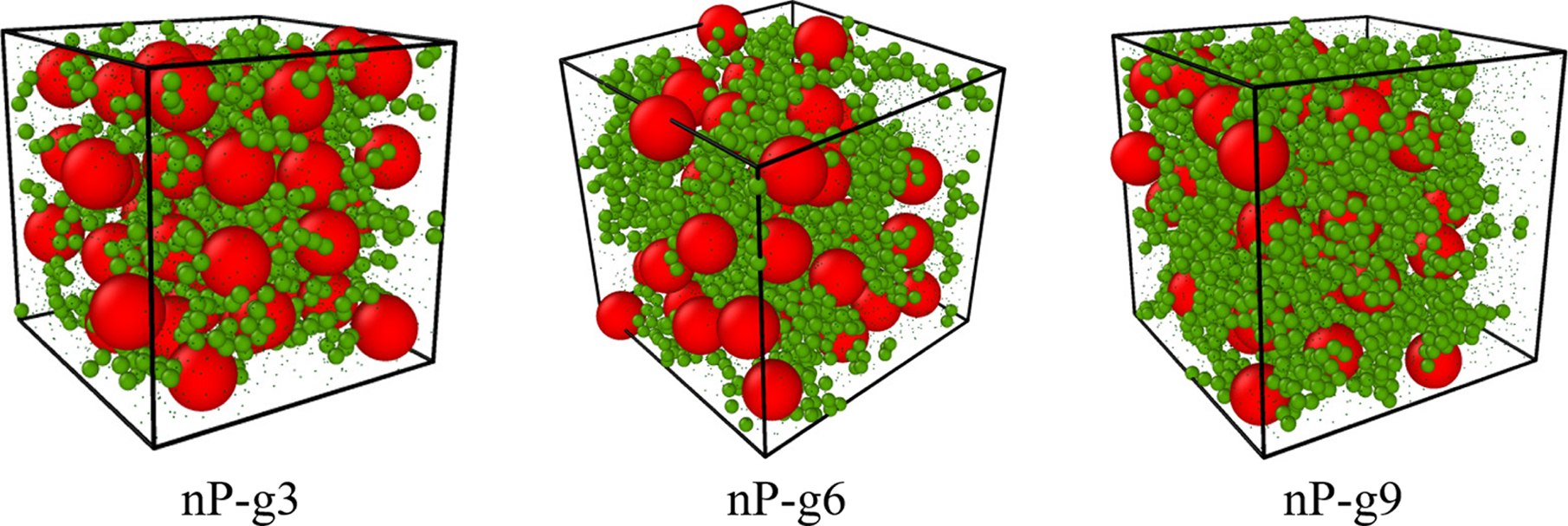
effectively strengthen the polymer matrix. For better illustration, the
snapshots of the coating status of different grafting chain lengths on the filler
are shown in Figure 8. Note that the polymer chains are represented by olive
points to avoid obscuring the nanoparticles, the red spheres denote the
fillers, the green spheres denote graft chains. These snapshots also
intuitively display that the longer the graft chain is, the more the filler
surface is coated.
|
Figure 1 Temperature of glass transition (Tg) of polymer composites filled with different types of filler particles (nP, gP and cP,
respectively). Filling degree is 1.34%. |
|
Figure 2 Effect of filling degree on the mechanical properties of
grafted particle and primary particle filled rubber composites. |
|
Figure 3 Effect of filling degree on mechanical properties of network of particles and primary filled rubber composites. |
|
Figure 4 Hysteresis loop of loading and unloading stress-strain
curves. |
|
Figure 5 Effect of different filler loading on the grafted particle,
network of particles and primary particle systems to hysteresis area. |
|
Figure 6 Effect of graft chain length on the grafted particle and network of particles to the mechanical properties. |
|
Figure 7 Effect of graft chain length on the network of particles to
hysteresis area |
|
Figure 8 Snapshots of polymer composites filled with grafting chains with lengths to be 3 beads (nP-g3), 6 beads (nP-g6) and 9 beads (nPg9), respectively. |
The effects of three different types of filler particles on the
mechanical and heat generation properties of polymer composites were studied by
molecular dynamics simulation. The results show that the surface modification
onto filler particles can reduce the friction between filler particles, and so
to restrain the heat generation of polymer composites in dynamic process. A
moderate cross-linked filler particles network may effectively strength polymer
matrix. To design an ideal network of cross-linked filler particles in polymer
composites can make a polymer material with wonderful mechanical and heat
generation properties.
Acknowledgements: The authors acknowledge the support from National Key
R&D Program of China (No. 2017YFB 0406204), National Natural Science
Foundation of China (No. 51973002) and University Institution of High
Performance Rubber Materials of Anhui Province.
- 1. Z. H. Tang, L. Q. Zhang, W. J. Feng, B. H. Guo, F. Liu, and D. Jia, Macromolecules, 47, 8863 (2014).
-

- 2. S. J. Park, J. Y. Kang, and S. K. Hong, Polym. Korea, 29, 151 (2005).
- 3. C. Nah and B.W. Jo, Polym. Korea, 23, 271 (1999).
- 4. A. I. Medalia, Rubber Chem. Technol., 64, 481 (1991).
-

- 5. A. M. Kucherskii, Polym. Test., 24, 733 (2005).
-

- 6. T. V. M. Ndoro, E. Voyiatzis, A. Ghanbari, D. N. Theodorou, M. C Böhm, and F. Müller-Plathe, Macromolecules, 44, 2316 (2011).
-

- 7. J. X. Shen, J. Liu, Y. Y. Gao, D. P. Cao, and L. Q. Zhang, Langmuir, 27, 15213 (2011).
-

- 8. C. Mahoney, C. M. Hui, S. Majumdar, Z. Y. Wang, J. A. Malen, M. N. Tchoul, and K. Matyjaszewski, Polymer, 93, 72 (2016).
-

- 9. M. Mahmoudian, E. Nozad, and M. Hosseinzadeh, Polym. Korea, 42, 434 (2018).
-

- 10. S. J. Park, K. S. Cho, and S. K. Ryu, Carbon, 41, 1437 (2003).
-

- 11. Y. Q. Tan, L. J Fang, J. L Xiao, and Q. Zheng, Polym. Chem., 4, 2939 (2013).
-

- 12. I. J. Jang, J. H. Jeong, and J. W. Jeong, Polym. Korea, 41, 741 (2017).
-

- 13. X. Ye, M. Tian, and L. Q. Zhang, J. Appl. Polym. Sci., 124, 927 (2012).
-

- 14. Q. Li, X. Li, S. H. Jang, D. H. Lee, Y. Fan, and U. R. Cho, Polym. Korea, 41, 1027 (2017).
-

- 15. J. Kim, H. Im, J. Han, and J. Kim, Polym. Korea, 36, 22 (2012).
-

- 16. I. A. Rahman and V. Padavettan, J. Nanomater., 2012, 132424 (2012).
-

- 17. K. Kremer and G. S Grest, J. Chem. Phys., 92, 5057 (1990).
-

- 18. M. Kröger, Phys. Rep., 390, 453 (2004).
-

- 19. J. Liu, S. Z. Wu, L. Q. Zhang, W. C Wang, and D. P. Cao, Phys. Chem. Chem. Phys., 13, 518 (2011).
-

- 20. S. Plimpton, J. Comput. Phys., 117, 1 (1995).
-

- Polymer(Korea) 폴리머
- Frequency : Bimonthly(odd)
ISSN 0379-153X(Print)
ISSN 2234-8077(Online)
Abbr. Polym. Korea - 2023 Impact Factor : 0.4
- Indexed in SCIE
 This Article
This Article
-
2020; 44(6): 804-808
Published online Nov 25, 2020
- 10.7317/pk.2020.44.6.804
- Received on May 27, 2020
- Revised on Jul 18, 2020
- Accepted on Jul 29, 2020
 Services
Services
- Full Text PDF
- Abstract
- ToC
- Acknowledgements
Introduction
Models and Methods
Results and Discussion
Conclusions
- References
Shared
 Correspondence to
Correspondence to
- Peng Chen and Jia-Sheng Qian
-
College of Chemistry & Chemical Engineering, Institute of High Performance Rubber Materials & Products, and Key Laboratory of Environment-Friendly Polymeric Materials of Anhui Province, Anhui University, Hefei 230601, China
- E-mail: chenpeng@ahu.edu.cn, qianjsh@ahu.edu.cn
- ORCID:
0000-0003-4758-4552, 0000-0002-7534-4639










 Copyright(c) The Polymer Society of Korea. All right reserved.
Copyright(c) The Polymer Society of Korea. All right reserved.