- Air Venting Simulation for Multiphase Flow of Polymers and Air in the Cavity of a Mold
Hankook Tire Technodome, 50, Yuseong-daero 935beon-gil, Yuseong-gu, Daejeon 34111, Korea
*Department of Machanical System Design Engineering, Seoul National University of Science and Technology 232 Gongneungro, Nowon-gu, Seoul 01811, Korea- 고분자와 공기의 다상유동을 고려한 캐비티 내 공기 벤팅의 컴퓨터 모사
한국타이어 중앙연구소, *서울과학기술대학교 기계시스템디자인공학과
Air venting is important in
the polymer shaping process, which uses the cavity of a mold. Inadequate air
venting invokes a short shot and burn marks in the product. Therefore, it is
necessary to evaluate and predict the venting performance according to the vent
location and size when the material is introduced into the cavity. In this
study, a computer simulation was performed considering the multiphase flow to
examine the venting phenomena when the material flows into the cavity, which is
equipped with varying venting hole. The computer simulation predicted the
interface variation between the material and air as a function of time. The air
venting phenomena was analyzed when the occupying material pushed air into the
cavity. The suitability of venting can be evaluated using pressure and velocity
distribution of air in the venting region.
금형의 캐비티를 이용한 고분자 성형공정에서는 캐비티 내
공기의 벤팅이 중요하다. 부적절한 공기의 벤팅은 성형품에 충전부족, 탄화자국
등의 불량을 일으킨다. 따라서 캐비티 내에 재료가 채워질 때 벤트의 위치 및 크기에 따라 공기의 벤팅이
적절한지 예측하고 평가하는 방법이 필요하다. 본 논문에서는 가변 벤팅 홀을 포함하는 캐비티 내에서 재료의
유입에 의한 공기의 벤팅 현상을 다상유동을 고려하여 컴퓨터 모사를 시도하였다. 컴퓨터 모사를 통해 시간에
따라 변하는 재료와 공기의 경계면을 예측하였다. 그리고 재료가 캐비티 내에 채워지면서 공기가 재료에
밀려서 벤팅부로 빠져나가는 현상을 분석하였다. 벤팅부에서 공기의 압력과 속도분포를 이용하여 벤팅의 적절함을
평가할 수 있다
A computer simulation was performed considering the
multiphase flow to examine the venting phenomena when the material flows into
the cavity. The suitability of venting can be evaluated using pressure and
velocity distribution of air in the venting region of cavity.
Keywords: air venting, multiphase flow, variable vent hole, computer simulation, venting velocity
이 논문은 산업통상자원부 산업핵심개발사업으로 지원된 결과입니다(10051680,
3D 프린팅용 친환경 고강도 고분자 소재 개발).
고분자소재의 응용이
증가되면서 고분자제품의 성형이 활발히 진행되고 있다. 고분자성형은 고분자 용융체나 유연성 있는 상태의 소재를 금형의 캐비티 안에 채우면서 이루어진다.
대표적인 예가 사출성형, 블로우성형, 열성형, 그리고 타이어 성형에서 가류공정(shaping process) 등이다. 이때 캐비티 안에 있던 공기가 캐비티 밖으로
빠져나가면서 고분자재료가 채워지는데 벤팅(venting)은 제품의 성형에 크게 영향을 미친다. 공기가 캐비티 밖으로 빠져나가지 못하고 캐비티 내에
갖혀있게 되면 미성형이 된다. 또한 캐비티 안에 갖힌 공기가 단열압축되면서 온도가 크게 올라 재료를 탄화시킨다. 따라서 고분자 성형공정에서 공기의 벤팅은 매우 중요하다.1
고분자제품의 형상이
복잡해지면서 캐비티 내의 흐름이 복잡해지고 공기의 흐름 역시 복잡하다. 따라서 캐비티 내 공기의 벤팅을 예측하는 것은 쉽지 않다. 공기의 벤팅을
예측하기 위해서 컴퓨터해석이 응용되고 있는데 이는 캐비티 내에 흐르는 고분자 수지의 흐름을 보면서 공기의 벤팅을 예측하는 수준이다.2-6
실제로는 캐비티 내에 고분자 용융체와 공기가 공존하기 때문에 두 물질의 흐름을 모사하여 공기의 벤팅을 예측하여야 하는데 이의 연구는 아직 초보단계이다.7
본 연구에서는 캐비티
내의 공기의 벤팅 현상을 예측하기 위해서 고분자재료와 공기를 동시에 포함하는 다상유동해석 방법을 사용하였다.8 캐비티 내 벤팅 영역의 크기가 일정하지 않고 변화하는 벤팅 구조에서 고분자재료가 흘러 들어오면서 공기가 밀려 벤팅 영역으로 빠져나가는 현상을 모사하였다.
VOF(volume of fluid) 방법을 사용한 고분자재료와 공기의 다상유동해석으로 캐비티 내의 공기가 빠져나가는 경로와 속도, 압력분포를
관찰하였다. 이러한 다상유동해석 방법은 많은 고분자 성형공정에 응용할 수 있으며, 캐비티 내 공기의 벤팅을 이해하고 벤팅 시스템을 설계하는데 응용할
수 있을 것으로 판단된다.
연구모델. 연구모델은 Figure 1과 같이 사각형상을 갖는 캐비티와 캐비티 아래에 벤팅을 위한 홀을 갖고 있는 형상이다. 형상의 대칭성을 고려하여 1/4영역을 해석에 사용하였다. 벤팅 홀을 갖는 벤팅 영역 내에서는 수직방향(Z방향)으로 움직일 수 있는 가변벤트
구조물이 포함되어 있다. 가변벤트 구조는 벤트핀과 스프링으로 구성되어 있다.
벤트핀이 벤팅 홀에서 돌출되어 있어 벤팅 홀이 열려 있다가 재료가 캐비티를 채우면서 벤트핀 머리에
닿으면 압력이 가해진다. 이때 벤트핀을 누르는 힘이 스프링의 탄성력을 넘어서면 벤트핀이 움직이면서 최종적으로 벤팅 홀을 닫아주는 구조이다. Figure 1에서는 스프링을
제외한 케비티, 벤트핀, 벤팅 홀의 모델링을 나타내고 있다.
캐비티 내에 공기를
고려한 고분자재료의 흐름을 컴퓨터 모사할 수 있도록 모델링하였으며 고분자재료는 타이어에 사용되는 고무를 사용하였다. 시간이 지남에 따라 사각 형상을
갖는 캐비티의 윗쪽에 있던 고무가 아래방향(-Z방향)으로 내려오고 공기가 재료에 밀려서 벤팅 홀을 따라 빠져나가는 현상을 관찰하고자 했다. 고무의
흐름이 계속 진행되면서 고무가 가변벤트의 벤트핀을 누르면서 핀이 벤팅 홀을 따라 내려가게 되고, 결국 재료가 캐비티에 완전히 채워지면서 벤팅 홀이
닫히게 되는 현상을 구현하고자 했다.
본 연구에서는 상용
CFD(computational fluid dynamics) 프로그램인 Fluent(ANSYS 사)를 사용하여 캐비티 내의 고무와 공기의 다상유동
해석을 비정상 상태로 모사하였다. 또한 해석모델 내에 스프링 반발력을 갖는 벤트 구조물이 자유도를 갖고 벤팅 영역을 열고 닫을 수 있게 시스템을 구성했다.
다상유동의 지배방정식 및 재료모델. 다상유동의 지배방정식은 연속방정식, 운동량 방정식, 이송방정식이며
식 (1), (2), (3)과 같이 표현된다.
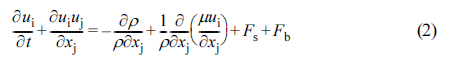

Fs는 표면의 힘, Fb는
체적 힘을 의미하며 f 는 액체의 부피이다. fi,j,k는
각 i, j, k번째 격자 내에서 차지하는 유동체의 부피비로 식 (4)와 같이 정의된다.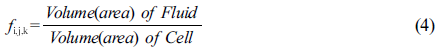
fi,j,k 값이 1이면 유동체, 0이면 기체, 0과 1 사이면 두 상의 경계를 의미한다. fi,j,k ΔxΔyΔz는 (i, j, k)번째 격자에서 유동체가 차지하는 부피가 되고, 기체는
(1 - fi,j,k)ΔxΔyΔz이다. 각 격자에서 상의 부피비가 계산되며 밀도와 점성계수는
각각 식 (5)와 식 (6)과 같이 정의한다.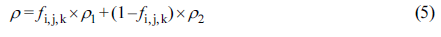
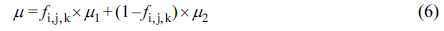
ρ1, μ1는 유동체의
밀도와 점성계수, ρ2, μ2는 기체의
밀도와 점성계수이다. 해석에 사용된 공기와 고분자재료의 물성이 Table 1에 나타나 있다.
공기의 경우 표준대기
조건에서 밀도와 점도를 적용했다. 고무는 물성을 측정하여 적용하였다(RPA 2000, Alpha technologies). 고무의 점도는 식
(7)과 같이 표현되는 Cross law model을 사용하였으며 curve fitting 결과가 Figure 2에 나타나 있다.
Cross law
model은 전단변형률 속도에 따른 점도의 함수이며 η0는 초기
점도(0.124 MPa·sec), λ는 이완시간(1 sec), 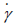 는 전단변형률 속도, 1-n(n=0.3)은 Cross law index를 나타낸다.
는 전단변형률 속도, 1-n(n=0.3)은 Cross law index를 나타낸다.
다상유동해석에서 완전하게
섞이지 않는 두 유동체들에 의해 형성되는 계면장력을 고려하기 위해 Antonoff’s rule을 사용하였다. 두 액체간의 계면장력(γAB)은 각각의 표면장력의 차(γA-γB)의
절대량과 같으며 식 (8)과 같이 계산된다.9 따라서 고무의 표면장력이 고무와 공기의 계면장력이라고 할 수 있다. 
본 연구에서 적용한
고무의 표면장력은 0.02 N/m를 적용했다.10,11
다상유체의 흐름을
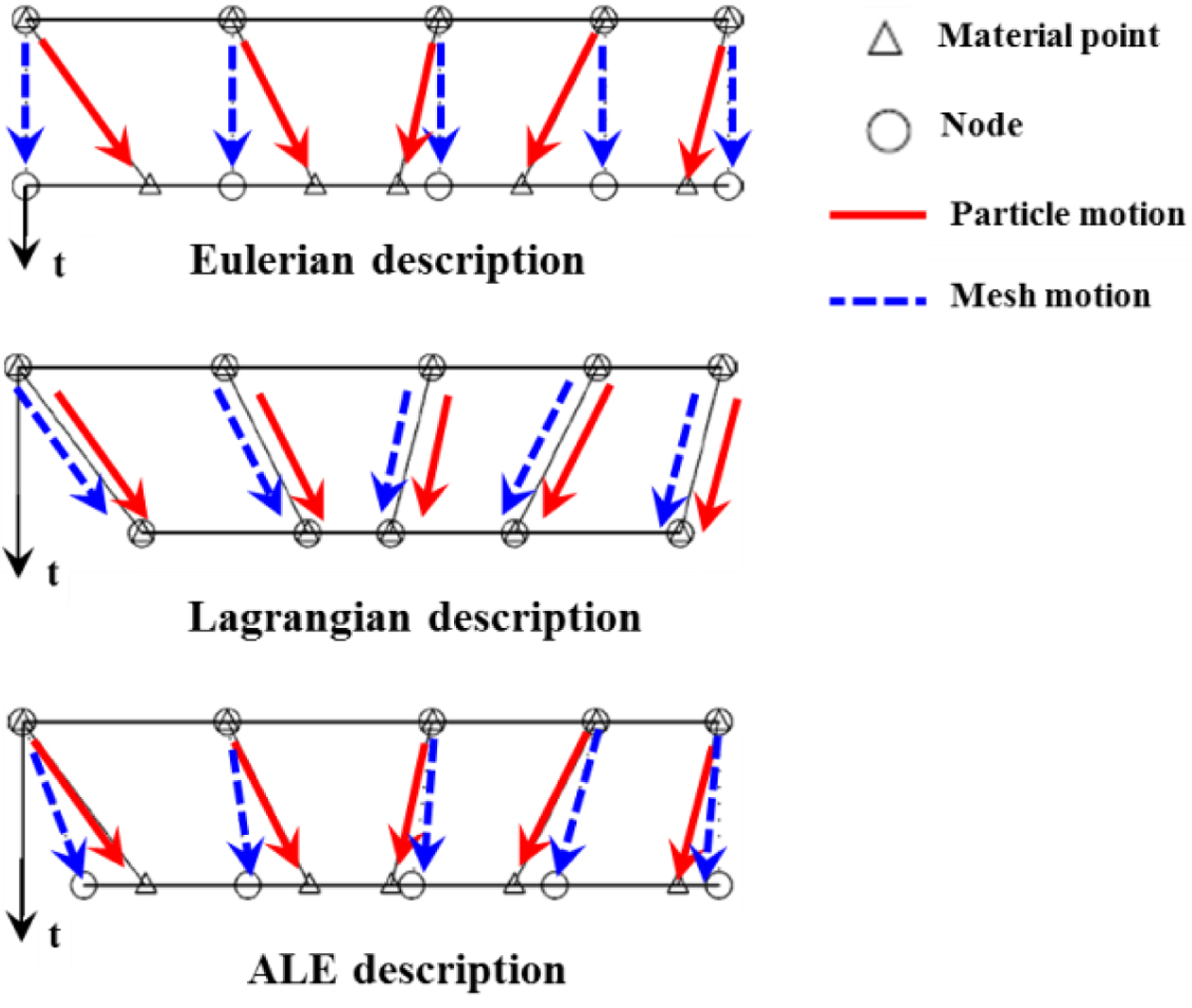
수치적으로 모사하기 위해서 ALE (arbitrary Lagrangian Eulerian) 방법을 채택하였다. Eulerian 방법은 계산하고자
하는 격자를 공간에 고정하고 움직이는 물질의 이동을 관찰하고, Lagrangian 방법은 물질에 격자를 두고 이동을 관찰한다. ALE 방법은 물질의
이동은 Lagrangian 방법, 격자의 이동은 Eulerian 방법을 사용하여 각 방법의 한계를 보완하고 장점만을 부각시킨 방법으로 알려져 있다.12,13
Figure 3에 ALE 방법이 도식적으로 나타나 있다.
경계면의 계산. 고분자재료와 공기와 같이 밀도 차이가 큰 두 재료의 컴퓨터
모사는 경계면을 기준으로 국소 물성 값이 급격하게 변하게 되어 수치해석상의 어려움이 크다.14,15 재료들 간의 경계면을 컴퓨터 모사하기 위해서는 경계면의 변화를
수치적으로 계산해야 하는데 그
방법으로는 interface tracking과 interface capturing 방법이 사용되는데 본 연구에서는 interface
capturing 방법을 사용하였다.16-18
두 상의 경계면을
포착하는 interface capturing 방법은 volume of fluid(VOF) 방법과 level-set 방법이 대표적으로 쓰이고 있다.8,19-22 그 중 VOF 방법은 셀 또는 검사 체적 내에 체적 비의 개념으로 정의된
값을 사용하여 상 경계면을 계산하고 각 상의 체적 보존이 용이하다는 물리적인 장점이 있어 많이 사용되며 본 연구에서도 이 방법을 사용하였다. VOF 방법은 주로 비압축성 재료의 다상 유동의 모사에 광범위하게
사용되어 왔으며 식 (4)에 나타낸 유체의 체적분율(volume fraction, f )로 정의된 함수에 의해 0과 1사이의 값을 갖게 된다.8,23
격자 생성 및 경계조건. 해석에 사용된 격자 형상이 Figure 4에 나타나
있다. 두 가지 상의 경계면을 계산하는 VOF 방법의 계산과 해석모델의 격자 재생성 및 변형에 의해 발생하는 낮은 해석 수렴도를 높이기 위해 격자는
육면체로 형성하였고 총 격자 수는 470918개이다. 벤팅이 시작되는 가변 벤팅 홀 입구영역은 5개의 격자 층이 유지되도록 생성했다.
해석모델에 적용한
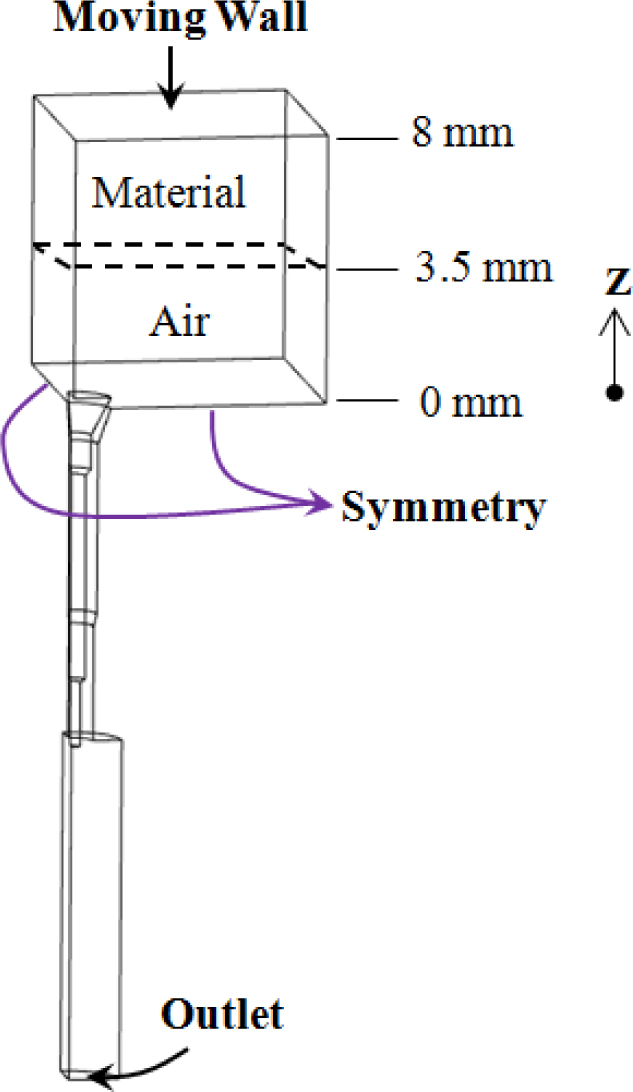
경계조건은 Figure 5에 나타냈다. 캐비티의 윗 면은 재료를 압축하는 벽면 형상을 모사하기 위해 수직 아래방향(-Z 방향)으로 moving
wall 조건을 적용하고
시간에 따른 위치를 정의하는 profile 구문을 사용했다. 벤팅 영역의 출구를 의미하는 outlet부에는 대기압 조건을 적용하고 1/4 대칭면에는
symmetry 조건을 적용했다. 그 외의 면은 wall 조건을 적용하였다.
해석모델(캐비티)
일부분에 재료가 가득 차 있는 초기 조건을 구현하기 위해서 Z좌표계 3.5~8 mm 영역에서 고무의 부피 체적율을 100%로 정의하였으며 이외의 영역(0~3.5 mm)은 공기영역으로 정의했다(Figure 5).
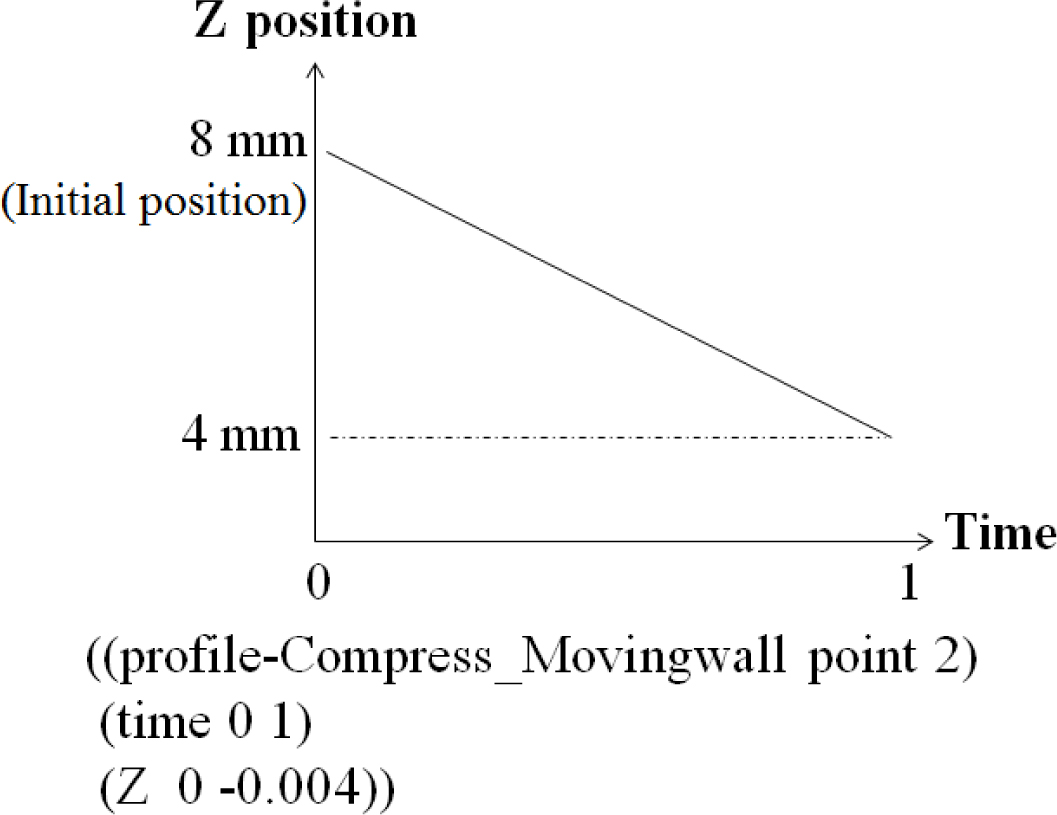
Figure 6에
해석모델의 윗 부분인 moving wall에 적용한 시간에 따른 위치 profile 구문을 나타냈으며 4 mm의 거리를 일정한 속도로 아래방향(-Z 방향)으로 내려오게 작성했다. 시간이 지남에 따라서
moving wall이 내려오며(-Z) 캐비티 윗쪽에 채워진 고무를 누르고 고무는 다시 공기를 누르게 되며 해석모델의 격자 역시 재생성된다.
격자의 재생성은
dynamic mesh의 layering method를 사용하였으며 collapse factor 0.2로 적용하여 격자 비율의 20% 수준에서
격자를 재생성하였다.
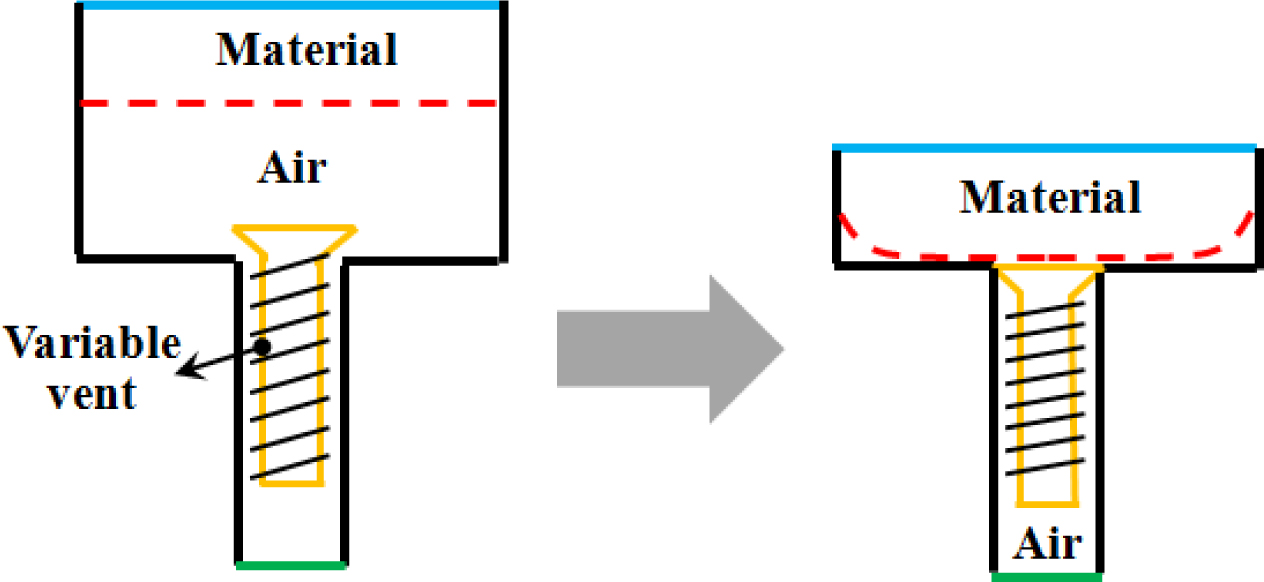
벤팅 밸브의 구동. Figure 7에 나타낸 벤팅 영역 내에 있는 가변벤트핀은
공기만 빠져 나가게 하고 재료가
벤팅 영역 내로 유입되는 것을 막는 역할을 한다. 이 가변벤트 구조물은 스프링을 포함하고 있는데, 내려오는 재료가 스프링의 힘보다 큰 힘으로 누르면
벤트핀은 벤팅 홀을 닫게 되고 재료가 벤팅 홀로 빠져나가는 것을 막는다. 즉, 재료가 캐비티에 채워지기 전까지는 벤트핀이 열려있어 벤팅이 잘 되고, 재료가 캐비티에 다 채워질 때는 벤트핀이 닫히게
되어 벤팅이 끝나고 재료가 캐비티에서 빠져나가지 않는다.
먼저, 가변벤트 구조물의
움직임을 고려하지 않고 시간에 따른 재료와 공기의 경계면 변화를 관찰하였다. 이는 재료가 벤트 구조물에 닿기 전까지 걸리는 시간 동안은 벤트 구조물이
움직이지 않는다고 가정할 수 있기 때문이다. 고정된 가변벤트 구조물에 압력이 높아지면 재료가 닿았다고 판단하고 닿기 직전 시간부터 스프링 반력을
갖는 가변벤트 구조물의 가동을 고려하였다.
벤트 구조물의 움직임을 고려하려면 자유도를 부여해야 하는데
이를 위해 6 degree of freedom(DOF) 방법을 적용하고user define function(UDF)을 통해 구현하였다. 6 DOF는
가변벤트 벨브의 질량, 관성
모먼트, 변위자유도, 회전자유도, 스프링상수, 그리고
가변벤트 벨브의 순간 변형거리로 구성했다. 이를 통해 재료가 가변벤트 벨브를 눌러 이동한 순간 변형거리가
스프링상수에 비례하여 가변벤트 벨브가 반발력을 갖도록 구현했다. Figure 8에 본 연구에서 사용한 UDF가 나타나있다. 스프링에 의한 반발력은 가변벤트 구조물이 재료의
누름에 의해 움직인 거리와 스프링 강성에 비례하도록 작성했다. 본 연구에서 적용한 스프링 강성은 2000, 8200 N/m 두 가지를 적용하였다.
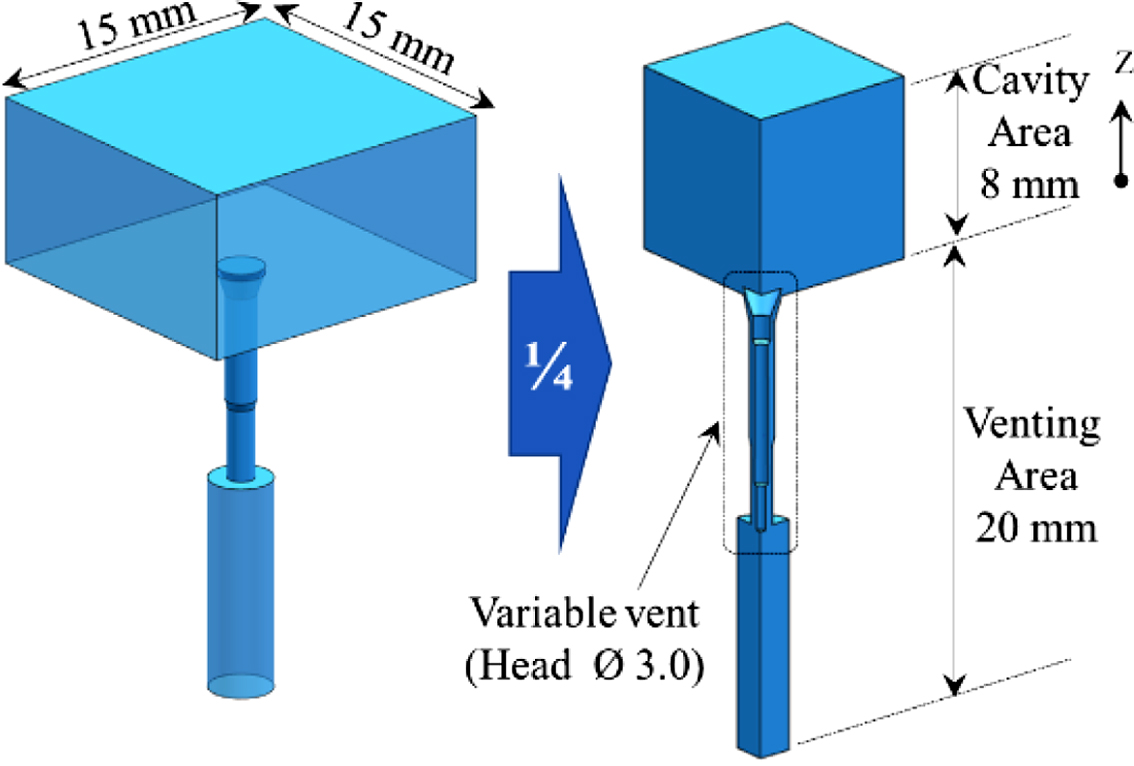
|
Figure 1 Study model for the multiphase flow simulation including varying venting hole. |
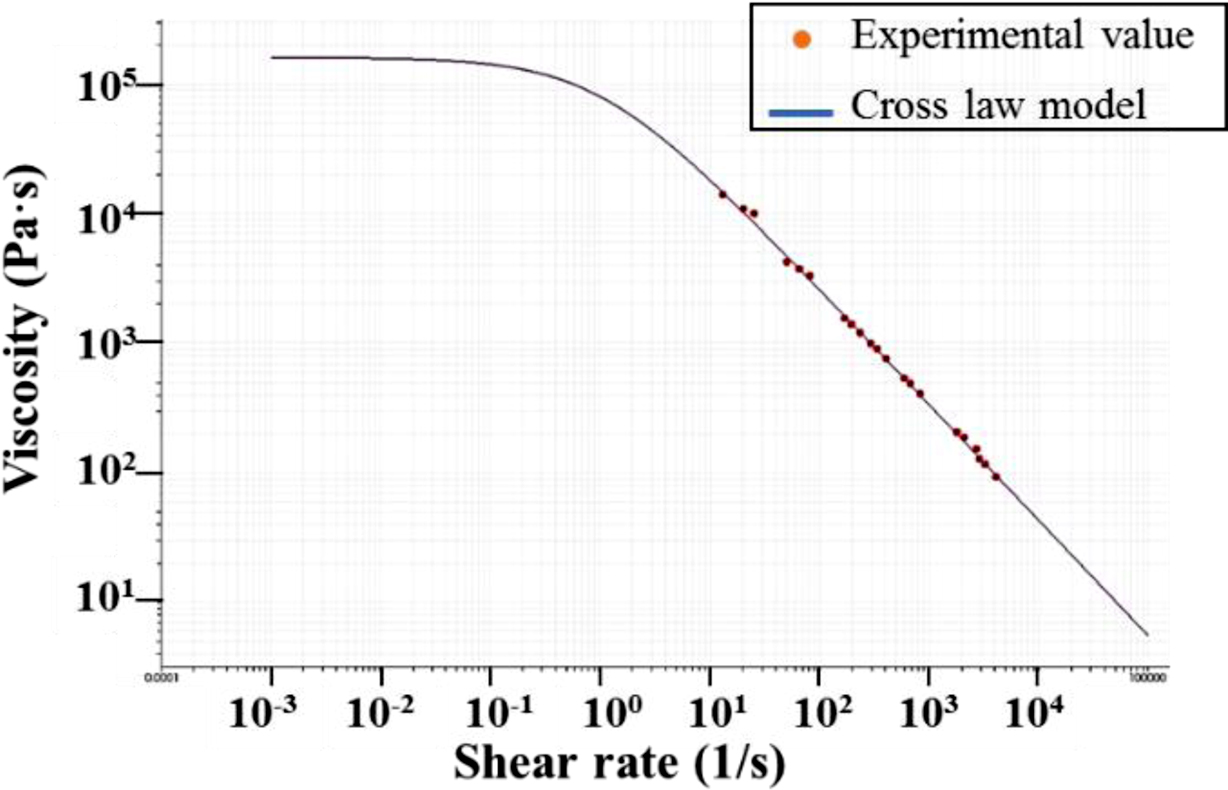
|
Figure 2 Measured shear viscosity curve and curve fitting with the Cross law model. |
|
Figure 3 Simulation method for a multiphase flow. |

|
Figure 4 Mesh for multiphase flow simulation. |
|
Figure 5 Boundary conditions in the cavity for simulation. |
|
Figure 6 Position profile for the moving wall according to time. |
|
Figure 7 Schematic drawing of the varying vent hole in the cavity. |

|
Figure 8 User define function (UDF) cording for variable vent with spring constant at 2000. |
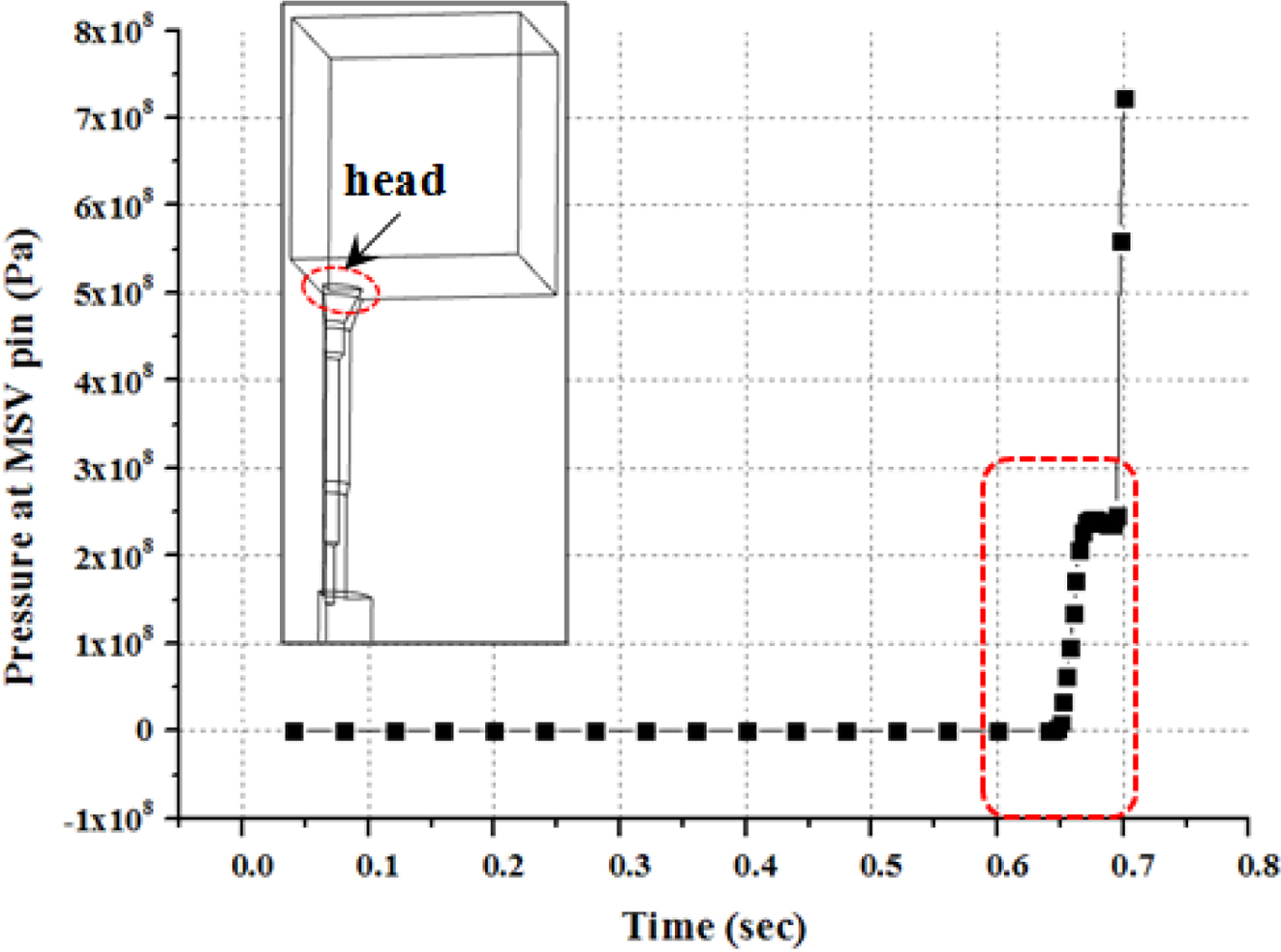
벤팅 구조물의 운동. Figure 9는 고정된 벤트핀 머리부의 시간에 따른 압력을 나타내고 있다. 해석이 진행되면서 재료는 벤트핀 방향으로 내려오게 되지만 약 0.6초 이전까지는 재료의 누름에 의한 압력이 나타나지 않는다. 하지만, 약 0.6~0.7초 사이에서 벤트핀 머리부에 압력이 급격히 증가하는데 이를 통해 약 0.6초 이후부터 재료가 벤트핀 머리부에 닿았다고 판단할 수 있다. 따라서 0.6초부터 스프링 반발력을 갖는 벤팅 구조물을 고려하였으며 스프링 강성에 따른 재료와 공기의 경계면 변화를 관찰하였다.
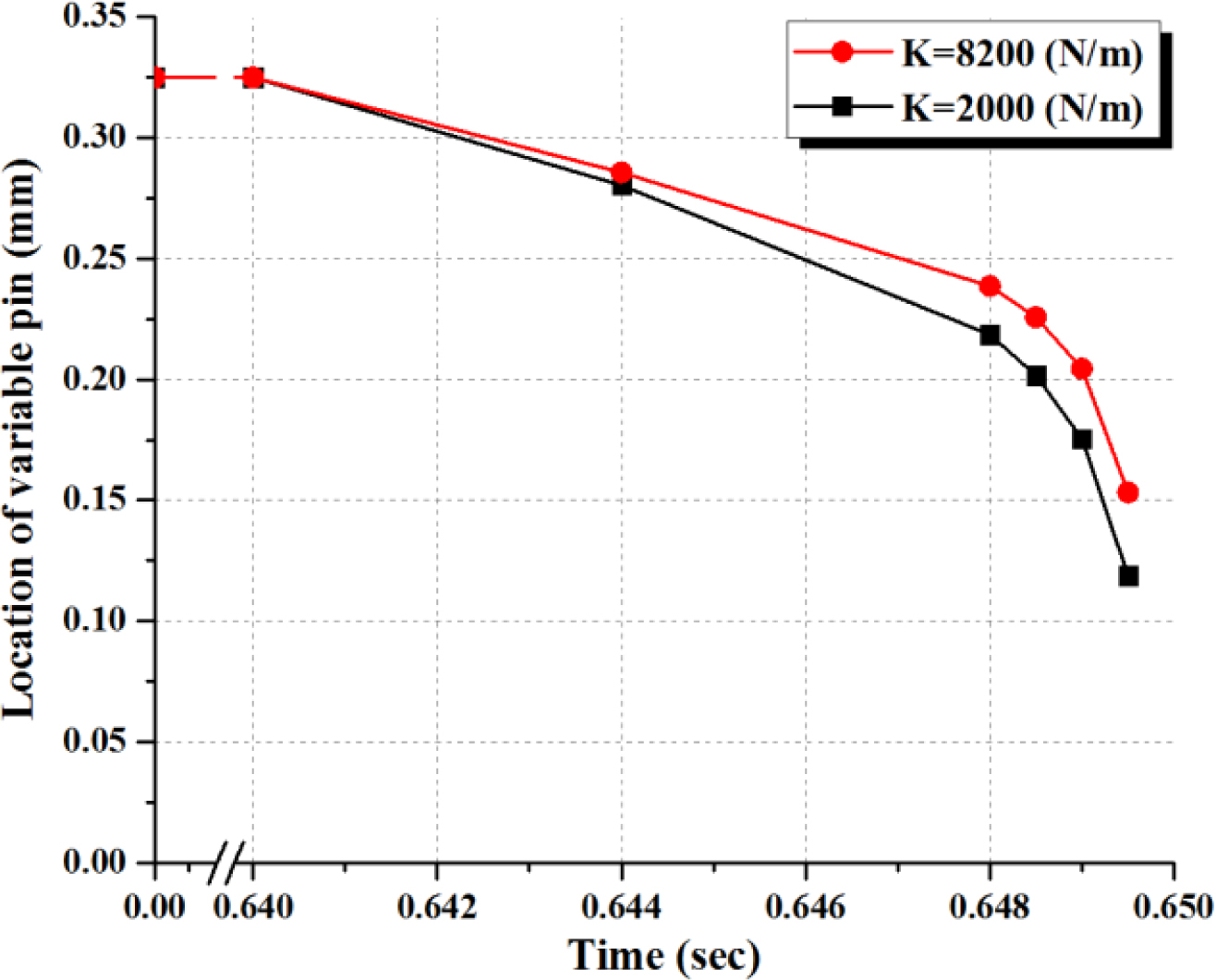
Figure 10에 벤트핀 머리부의 시간에 따른 위치(Z 좌표계) 를 나타냈다. 0~0.6초에서 고정된 벤트핀의 위치는 초기 돌출 높이인 0.325 mm이며 벤팅 영역이 열려 있는 상태다. 0.64초부터 재료의 누름에 의해 벤트핀의 위치는 시간에 따라 낮아지고 점차 닫히게 된다. 0.6495초에서 스프링 강성이 2000 N/m일 때 벤트 구조물의 닫힘 정도는 약 63% 정도이며, 스프링 강성이 8000 N/m일 때는 약 53%로 스프링 강성이 작은 경우에 더 많이 닫히게 된다. 벤팅 홀이 완전히 닫히기 직전(0.650초가 되기 전)에 해석은 종료된다.
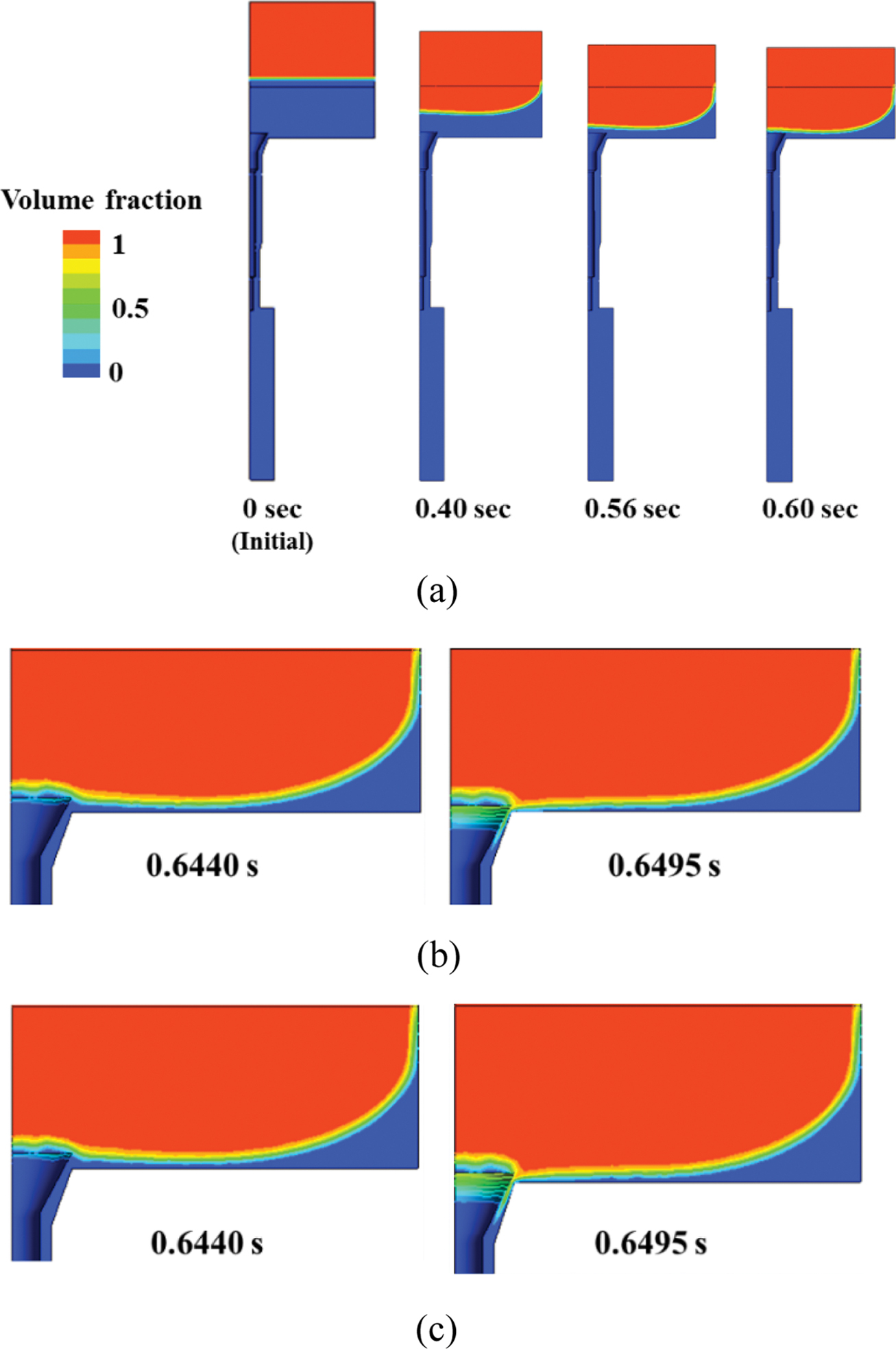
경계면의 변화. Figure 11은 금형 내에 시간에 따른 재료와 공기의 체적분율을 나타내고 있다. 체적분율이 1에 가까울수록 재료의 영역임을 나타내고 0에 가까울수록 공기의 영역을 나타낸다. 재료가 흘러 내려오면서 공기와 재료의 경계면이 0.6초까지 내려가고 있으며 Figure 11(a)에 나타냈다. 0.6초부터 0.6495초까지 스프링 강성에 따른 해석 결과를 Figure 11(b)와 11(c)에 나타냈다. 재료와 공기의 체적분율 분포를 통해 벤팅 홀 내부로의 재료 유입 정도는 스프링 강성에 따라 유의미한 차이가 나타나지 않았다. 하지만, 벤팅 영역으로 유입된 재료를 정량적으로 비교하기 위해 0.6495초에서 벤팅 구조물 면적에 재료의 체적분율을 계산했을 때, 스프링 강성 2000 N/m에서는 5.3%, 8200 N/m에서는 6.0%의 재료가 벤팅 구조물에 나타났다. 이는 벤팅 영역 내부로 재료가 유입되는 정도가 스프링 강성이 클 때 열리는 시간이 길어서 재료유입도 큼을 보여준다.
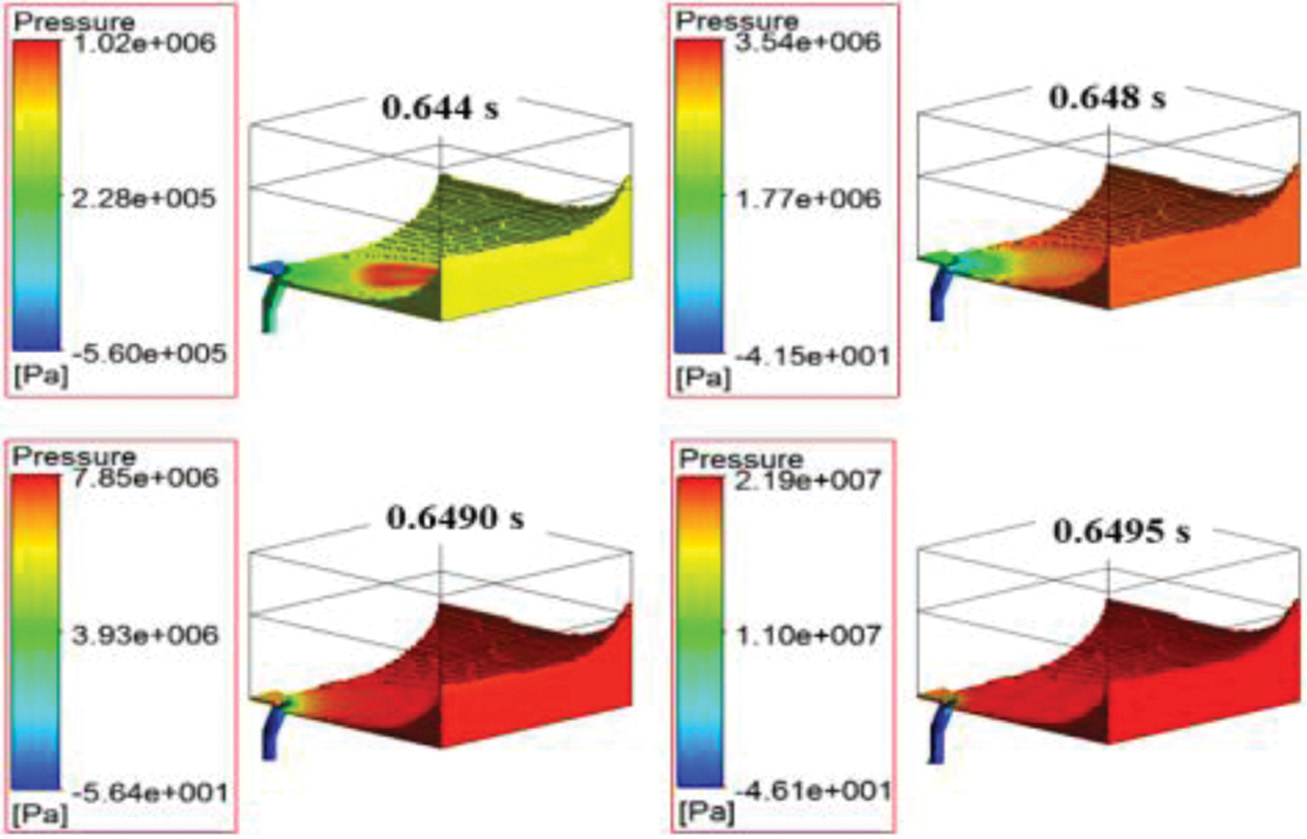
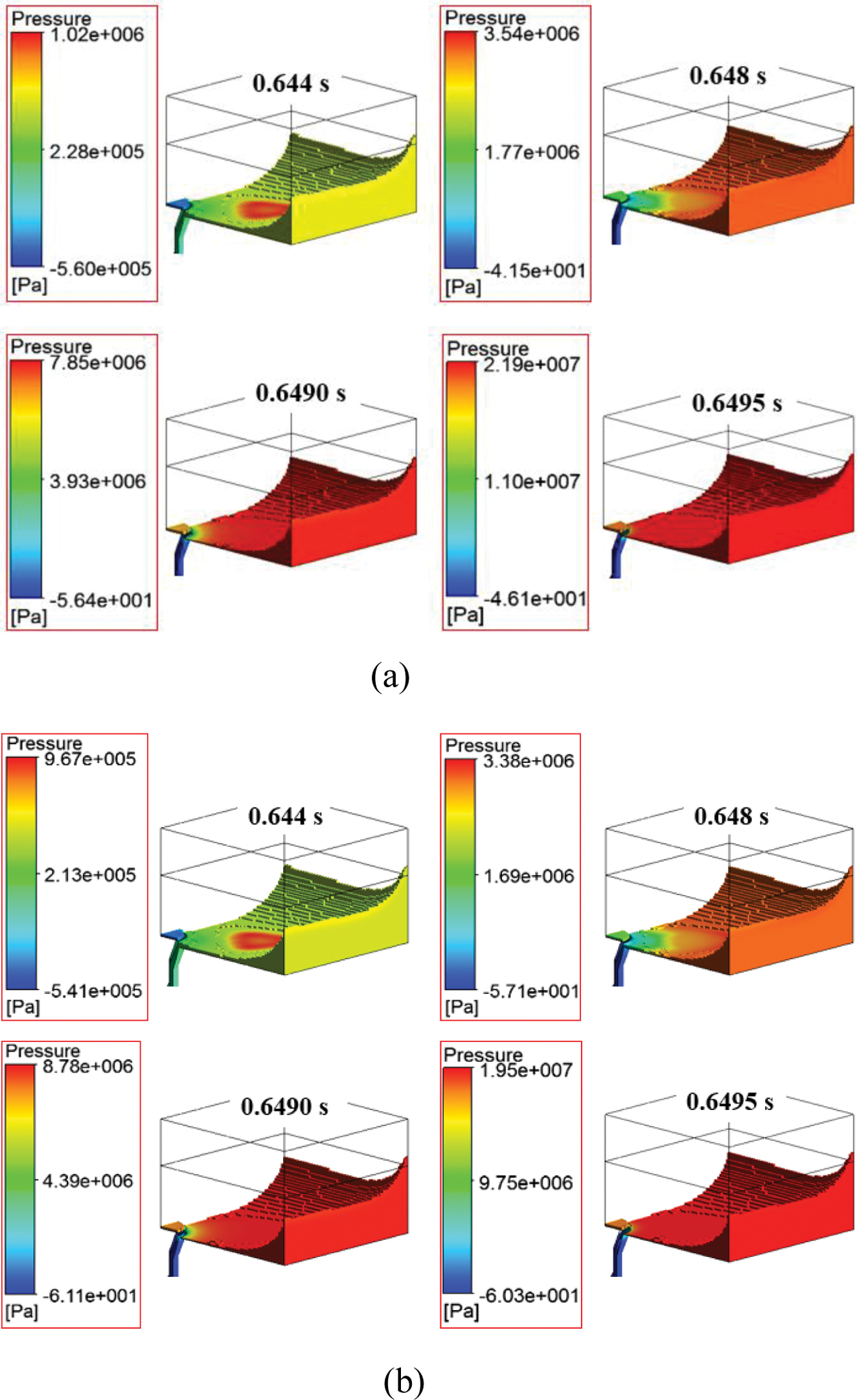
공기의 압력분포. Figure 12는 공기의 체적분율이 0.9 이상의 부피 영역에서 캐비티 내부의 압력분포를 시간에 따라 나타냈다. 스프링 강성이 상대적으로 작은 2000 N/m의 경우 캐비티 내부에서 0.644초일 때 캐비티 내에 공기의 최대 압력은 1.02×106 Pa으로 나타났으며 0.648초에서는 3.54×106 Pa, 0.649초에서는 7.85×106 Pa, 그리고 0.6495초에서는 2.19× 107 Pa로 관찰되었다. 시간이 지남에 따라 가변벤트의 닫힘과 재료의 유입에 의해 캐비티 내부의 공기 압력은 점차 증가하고 있다. 스프링 강성이 상대적으로 큰 8000 N/m의 경우 캐비티 내부 공기의 최대 압력은 0.644초에서 9.67×105 Pa, 0.648초에서 3.38×106 Pa, 0.649초에서 8.78×106 Pa, 그리고 0.6495초에서는 1.95×107 Pa로 관찰되었다. 같은 시간에서 스프링 강성이 큰 경우 캐비티 내에 공기의 압력은 스프링 강성이 작은 경우보다 상대적으로 작게 나타났다. 상대적으로 스프링 강성이 크면 스프링에 의한 반발력이 커서 가변 벤트핀이 보다 오래 열려 있음을 의미한다(Figure 10). 따라서 공기가 벤팅되는 영역이 상대적으로 넓어지고 공기의 벤팅이 보다 잘 되어 캐비티 내부의 공기의 압력이 작게 나타난 것으로 판단된다.
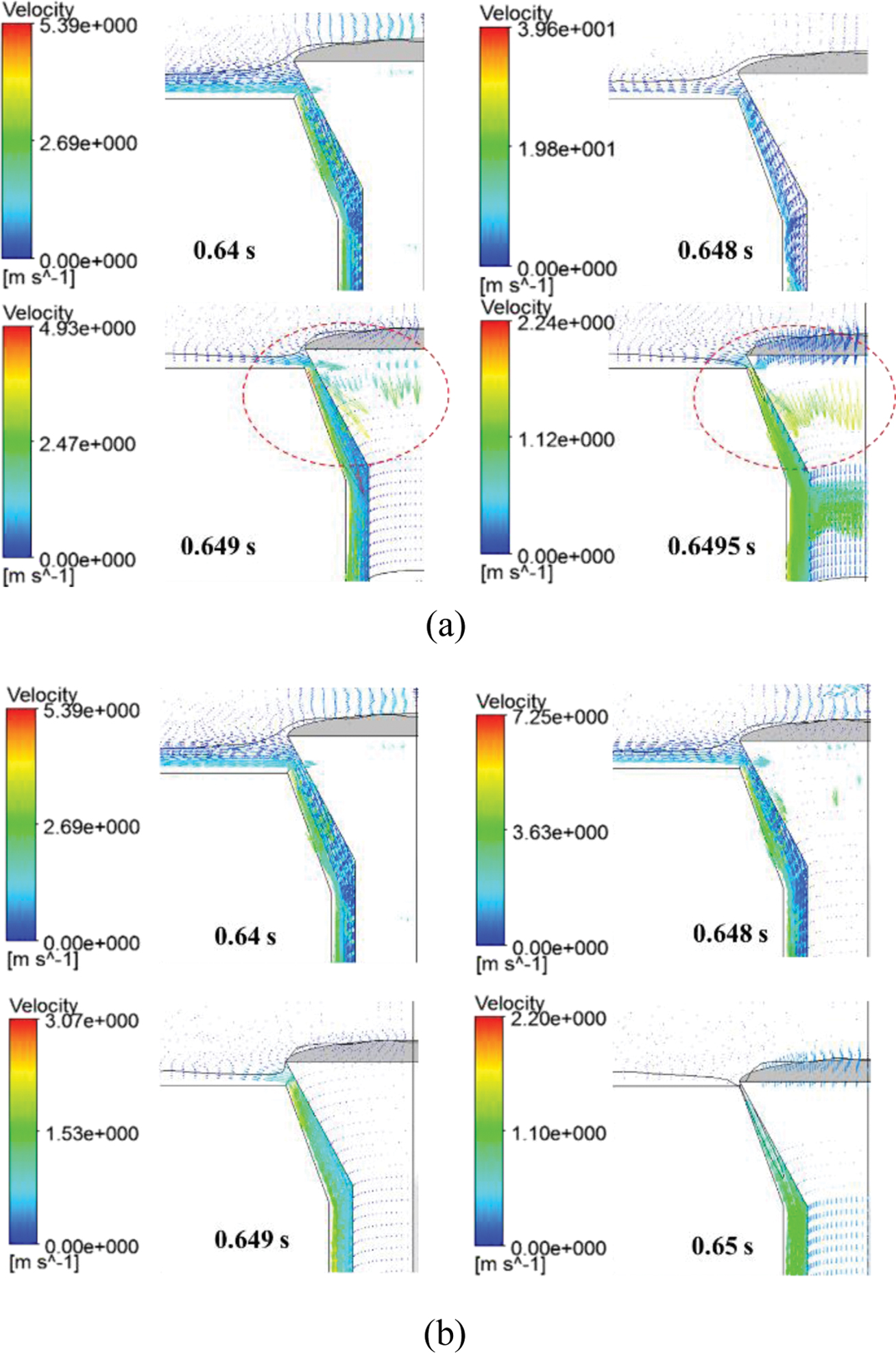
공기의 벤팅 속도. Figure 13은 공기의 체적분율이 0.9 이상의 부피 영역에서 가변벤트 입구의 속도분포를 시간에 따라 나타냈다. 스프링 강성이 상대적으로 작은 2000 N/m의 경우 가변벤트 영역 주변에서 0.64초일 때 0~5.39 m/sec의 벤팅 속도가 분포하지만 0.648초에서는 0~30.96 m/sec로 속도가 크게 분포했다. 0.649초에서는 0~4.93 m/sec로 벤팅 속도가 작게 분포하며 가변벤트 영역 입구 부분에서 공기의 방향이 복잡하게 나타났다. 또한 0.6495초에서도 공기의 방향이 더 복잡하게 나타나며 0~2.24 m/sec의 벤팅 속도가 나타났다. 캐비티 내로 재료의 충전이 진행됨에 따라 핀이 내려가면서 공기가 빠져나가는 통로가 좁아져 속도가 갑자기 증가한다. 그후 벤트핀이 더 닫히게 되면 벤팅 홀로 공기의 유입이 줄어들고 핀 주위의 벤팅 속도가 감소하며 방향이 균일하지 않게 된다.
스프링 강성이 상대적으로
큰 8200 N/m의 경우 가변벤트 영역 주변에서 0.64초일 때
0~5.39 m/sec로 벤팅 속도가 분포하고 0.648초에서는 0~7.25 m/sec로 벤팅 속도가 나타났다. 0.649초에서는 0~3.07 m/sec로 벤팅 속도가 분포하고 0.65초에서는
0~2.20 m/sec의 벤팅 속도가 나타났다. 스프링 강성이 클수록
핀의 닫힘이 늦어 벤팅 통로가 커서 벤팅 속도가 작게 나타났으며 방향도 규칙적으로 나타났다. 이는 스프링 강성이 클수록 상대적으로 가변벤트 구조물의
벤팅 영역이 넓어서 벤팅 속도가 낮고 규칙적인 방향으로 공기가 벤팅된 것으로 판단된다. 스프링 강성이 커서 핀이 닫히는 속도가 느려서 스프링 강성이
작은 경우에 나타나는 갑작스런 벤팅 속도의 증가는 관찰되지 않았다. 이는 적절한 벤팅 영역의 크기가 존재함을 의미한다.
|
Figure 9 Simulation results of the pressure at the head of the pin according to time. |
|
Figure 10 Location of the pin head in the venting hole according to time. |
|
Figure 11 Simulation results for the interface between the material and air according to time: (a) during 0~0.6 sec for spring constant of 2000 N/m; (b) spring constant of 2000 N/m; (c) spring constant of 8200 N/m. |
|
Figure 12 Pressure distribution of air according to time for various spring constants: (a) spring constant of 2000 N/m; (b) spring constant of 8200 N/m. |
|
Figure 13 Venting velocity distribution according to time: (a) spring constant of 2000 N/m; (b) spring constant of 8200 N/m. |
대부분의 고분자 성형공정(사출성형,
블로우성형, 압축성형, 열성형
등)은 캐비티 내에서 공기가 벤팅되면서 고분자재료가 캐비티를 채우고 성형이 된다. 즉, 캐비티 내의 공기를 고분자재료로 대체하는 것이다. 본 연구에서는
캐비티 내에 공기와 재료가 혼재할 때 재료의 움직으로 공기가 벤팅되는 현상을 컴퓨터 모사하였다.
캐비티 내의 공기의
벤팅을 효과적으로 하기 위해서 벤팅 홀의 크기가 변화하는 구조를 채택하는 경우가 있는데, 본 연구에서는 이를 고려하여 공기와 고분자재료의 경계면을
예측하고 공기가 벤팅되는 현상을 해석적으로 분석하였다.
벤팅 홀의 크기를
결정하는 핀의 움직임을 제어하는 스프링의 강성에 따라 해석결과는 다르게 나타났다. 강성이 클수록 벤팅 홀은 적게 닫혀 벤팅 영역이 크고, 강성이
작을수록 벤팅 홀은 더 많이 닫혀 상대적으로 벤팅 영역이 작게 나타났다. 또한 공기가 벤팅 홀을 통해 빠져나가고 나서 재료가 벤팅 홀을 빠져 나가는
현상도 나타났는데 스프링 강성이 클수록 컸다.
벤팅 영역이 큰 경우(스프링
강성이 큰 경우) 캐비티 내의 공기의 압력은 작고 벤팅 속도가 작게 나타났으며 벤팅 방향이 균일하였다. 반대로 벤팅 영역이 작은 경우(스프링 강성이 작은 경우) 캐비티 내의
공기의 압력은 크고 벤팅 속도가 크게 나타났으며 벤팅 방향이 벤팅 홀 입구에서 불균일하게 나타났다.
- 1. D. V. Rosato, D. V. Rosato, and M. G. Rosato, Injectionmolding handbook, 3rd Ed., Springer Science & Business Media, NewYork,2012.
- 2. C. Lotti, M. M. Ueki, and R. E. S. Bretas, J.Inject. Mold. Technol., 6, 157 (2002).
- 3. J. H. Mo, H. J. Kim, and M.-Y. Lyu, Elast.Compos., 38, 295 (2003).
- 4. S. T. Joo, Y. H. Kim, and M.-Y. Lyu, Trans. Mater.Process., 10, 525 (2001).
- 5. K.-H. Lim, Korean Chem. Eng. Res., 48,490 (2010).
- 6. B.-C. Song, S.-R. Kim, Y.-G. Kang, and M.-H. Ham, J.Korean Soc. Manuf. Process Eng., 10, 117 (2011).
- 7. J. W. Woo, K. M. Yang, and M.-Y. Lyu, Elast.Compos., 51, 263 (2016).
-

- 8. C. W. Hirt and B. D. Nichols, J.Comput. Phys., 39, 201 (1981).
-

- 9. S. Ghosh and H. B. Bull, Biochim. Biophys.Acta, 66, 150 (1963).
-

- 10. V. Broje and A. A. Keller, J.Colloid Interface Sci., 305, 286 (2007).
-

- 11. J.E. Mark, Polymer data handbook, Oxford University Press, NewYork, 1999.
- 12. T.B. Belytschko and J. M. Kennedy, Nucl. Eng. Des., 49, 17 (1978).
-

- 13. S.J. Kim, K. H. Lim, and C. Kim, Korean-Aust. Rheol. J., 18, 109(2006).
- 14. H. K. Myong, Trans. Korean Soc. Mech. Eng. B, 33,443 (2009).
- 15. K.-J.Lee, K.-S. Yang, and C.-W. Kang, J. Comput. Fluids Eng., 15, 99(2010).
- 16. J.E. Kim and H. K. Myong, J. Computat. Fluids Eng., 11, 14(2006).
- 17. W.J. Rider and D. B. Kothe, J. Comput. Phys., 141, 112(1998).
-

- 18. T. E. Tezduyar, Comput. Method. Appl. Mech.Eng., 195, 2983 (2006).
- 19. M. Sussmam, P. Smereka, and S.Osher, J. Comput. Phys., 114, 146 (1994).
-

- 20. Y. C. Chang, T. Y. Hou, B. Merriman, and S. Osher, J.Comput. Phys., 124, 449 (1996).
-

- 21. M. H. Cho, H.-G. Choi, and J.-Y. Yoo, Trans. KoreanSoc. Mech. Eng. B, 32, 754 (2008).
- 22. S. J. Kim and W. R. Hwang, J. Comput. Phys.,225, 615 (2007).
-

- 23. L. Zhou, D.-y. Liu, and C.-q.Ou, Eng. Appl. Comput. Fluid Mech., 5, 127 (2011).
-

- Polymer(Korea) 폴리머
- Frequency : Bimonthly(odd)
ISSN 0379-153X(Print)
ISSN 2234-8077(Online)
Abbr. Polym. Korea - 2023 Impact Factor : 0.4
- Indexed in SCIE
 This Article
This Article
-
2019; 43(6): 816-823
Published online Nov 25, 2019
- 10.7317/pk.2019.43.6.816
- Received on Feb 25, 2019
- Revised on Apr 2, 2019
- Accepted on Apr 2, 2019
 Services
Services
Shared
 Correspondence to
Correspondence to
- Min-Young Lyu
-
Department of Machanical System Design Engineering, Seoul National University of Science and Technology 232 Gongneungro, Nowon-gu, Seoul 01811, Korea
- E-mail: mylyu@seoultech.ac.kr
- ORCID:
0000-0001-7554-2072











 Copyright(c) The Polymer Society of Korea. All right reserved.
Copyright(c) The Polymer Society of Korea. All right reserved.