In this study, Monte Carlo n-patricle transport code (MCNP) simulation was used to derive equations that can be applied to all materials to calculate radiation shielding ability. The linear attenuation coefficient term, which ignores the interface in the composite material, was easily obtained by a well-known equation and was used in the simulation for more accurate calculation. The linear attenuation coefficients calculated by simulation show the same tendency in all materials regardless of g-ray energy. The value calculated by this tendency is considered to be the maximum value of the linear attenuation coefficient of composite material made of two materials.

본 연구에서는 MCNP(Monte Carlo n-patricle transport code) 시뮬레이션을 통해 다양한 재료 및 조건에 대한 차폐율을 계산해보고 이를 이용해 모든 재료에 적용해 차폐능을 계산할 수 있는 차폐 식을 도출하고자 하였다. 복합재의 구조를 생각하지 않은 선형감쇠계수항은 잘 알려진 식으로 쉽게 구할 수 있었으며 보다 실제와 비슷하게 계산하기 위해 시뮬레이션을 이용하였다. 시뮬레이션을 통해 계산된 선형감쇠계수는 감마선의 에너지 크기에 상관없이 모든 재료에서 같은 경향을 보였다. 이 경향으로 복합재의 선형감쇠계수를 계산할 수 있는 식을 도출해낼 수 있었다. 도출해낸 식으로 계산된 값은 두 재료로 이루어진 복합재가 가질 수 있는 선형감쇠계수의 최댓값으로 생각된다.

The linear attenuation coefficient term, what caused by just composition materials, was easily obtained by a well - known equation and was used simulation for more accurate calculation. The linear attenuation coefficients calculated by simulation show the same tendency in all materials regardless of γ-ray energy. The value calculated by this tendency is considered to be the maximum value of the linear attenuation coefficient of composite material made of two materials.

Keywords: radiation shielding, radiation attenuaion, Monte Carlo n-patricle transport code, linear attenuation coefficient, composite

이 논문은 2018년도 인하대학교의 지원에 의하여 연구되었음.

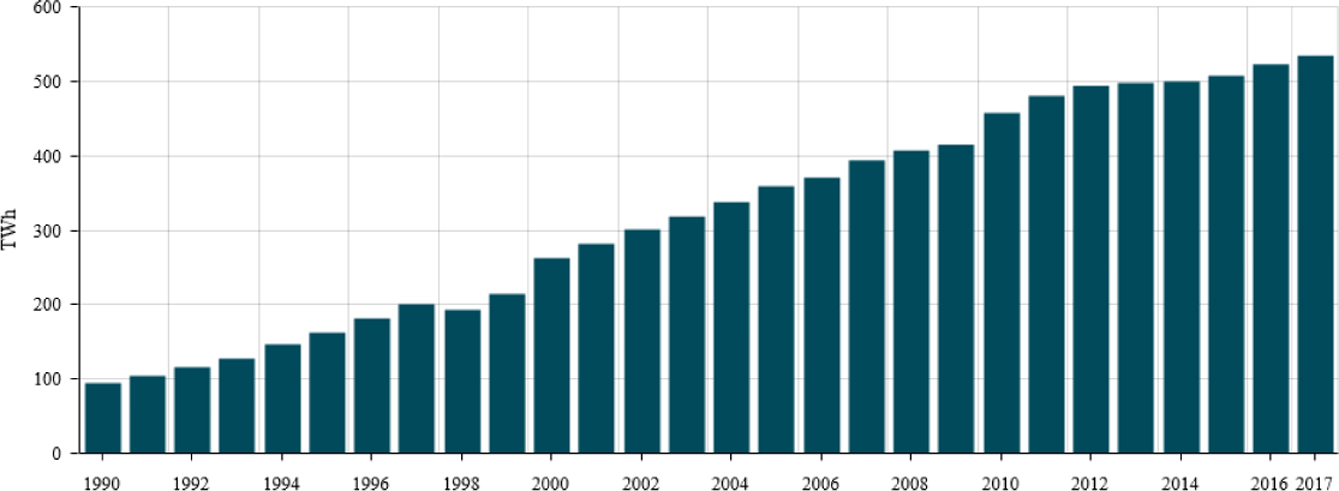
우리나라의 전기에너지 소비량은 1990년대부터 계속해서 증가하고 있으며(Figure 1) 그에 따라 다양한 형태의 발전소가 건설, 운영되고 있다. 그 중 원자력 발전소는 화력발전소와 수력발전소 다음으로 큰 비중을 차지하고 있다. 2016년 기준 전 세계 전력생산의 비중은 화력발전 67.3%, 수력발전 16.6%, 원자력발전 10.4%, 재생에너지 5.6% 등 이었으며 OECD 국가의 원자력 발전 비중은 17.7%에 달했다.^1,2
원자력발전의 비중이 세계적으로 높아지고 후쿠시마에서 원자력사고가 발생하면서 방사선의 위험성도 잇따라 조명되고 있다. 방사선의 위험성이 밝혀지면서 방사선 차폐에 대한 문제가 중요한 이슈로 대두되고 있으며, 이는 원자력 발전뿐만 아니라 의료분야, 반도체산업 등에서 방사선 사용이 많아지면서 더욱 많은 관심을 모으고 있다.
방사선 차폐는 병원에서 사용되는 방사선 장비에서부터 원전에서 발생되는 방사능폐기물까지 다양한 세기의 선원으로부터 인체를 보호하기 위해 꼭 필요한 기술이므로 다양한 연구자들이 이에 대한 연구를 진행하고 있다. 현재 다양한 재료 및 복합구조 재료의 차폐능이 분석되어 알려져 있으며, 이와 관련된 논문들이 출간되어 있다.^3-7
방사선은 인체에 유해하고 그 위험도가 높으므로 실험실에서 쉽게 다룰 수 없어 이를 이용한 실험은 모든 조건에서 실제로 진행하기가 어렵다. 또한 차폐재, 차폐구조물을 설치할 때 사전 설계가 필요하므로 이 단계에서 다양한 시뮬레이션을 사용하기도 하는데 가장 대표적으로 미국 핵무기 연구소에서 개발된 MCNP(Monte Carlo n-patricle code)가 있다. MCNP는 핵분열 프로세스 시뮬레이션에 주로 사용되지만 다른 입자들 사이에서 중성자, 광자 및 전자와 관련된 입자 상호 작용을 시뮬레이션할 수 있어, 방사선 선량 측정, 방사선 차폐, 방사선촬영 및 의학물리학, 방사선 검출기 설계 및 분석 등의 분야에서 사용된다.⁸
앞서 발표된 연구들은 모두 재료 및 복합구조를 한정하고 그에 대한 차폐능을 연구한 경우가 많아 다른 재료에 대해서는 적용하지 못한다는 문제를 가지고 있다. 따라서 본 연구에서는 MCNP 시뮬레이션을 통해 다양한 재료 및 조건에 대한 차폐율을 계산해보고 이를 이용해 모든 재료에 적용해 차폐능을 계산할 수 있는 차폐 식을 도출하고자 하였고 앞선 연구의 결과에 적용시켜 그 타당성을 입증하고자 하였다.

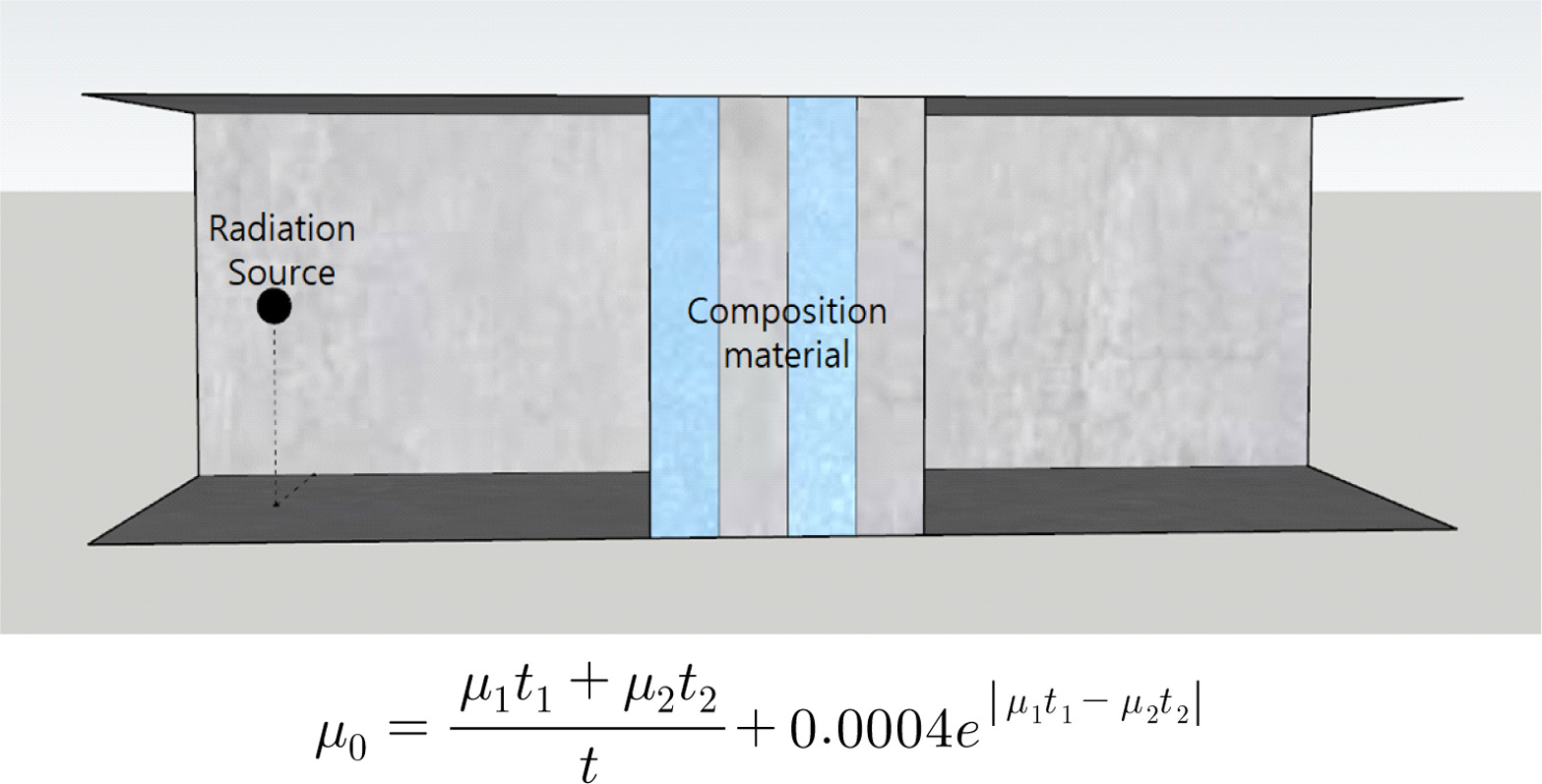
복합재의 형태. 차폐재에 한 가지 재료만을 사용할 경우 특별한 과정 없이 재료에 대한 선형감쇠계수를 알면 재료의 차폐능 계산이 가능하므로 두 가지 재료를 이용한 복합재형태로 시뮬레이션을 진행하였다. 또한 실재로 사용되는 복합재의 형태는 매우 다양하나 모든 복합재의 구조를 고려할 수는 없으므로 층상 복합재의 형태를 적용하였다. 이 때 단순한 복합구조를 보완하기 위해 복합재의 층상구조의 수를 2, 4, 8, 16, 32, 64 layer로 변화시켜가며 계면의 넓이를 다르게 하였다.
시뮬레이션 프로그램. 본 연구에서는 복합재의 선감쇠계수를 계산하기 위해 미국의 국립 연구소 RSICC(radiation safty information computational center)에서 배포하고 있는 MCNP6 코드를 사용하였다. MCNP는 방사성 입자와 어떠한 물질의 상호작용과 같은 현상을 통계적 접근을 통해 이론적으로 도출해낼 수 있으며 결정론적 방법의 컴퓨터 코드로는 모델링이 불가능한 복잡한 경우에도 적용이 가능하다.⁸
MCNP 코드를 이용한 시뮬레이션을 위한 input 파일에는 geometry를 정의하는 cell card와 surface card, 물질 및 선원에 대한 항을 정의하는 data card가 포함되어야 한다.
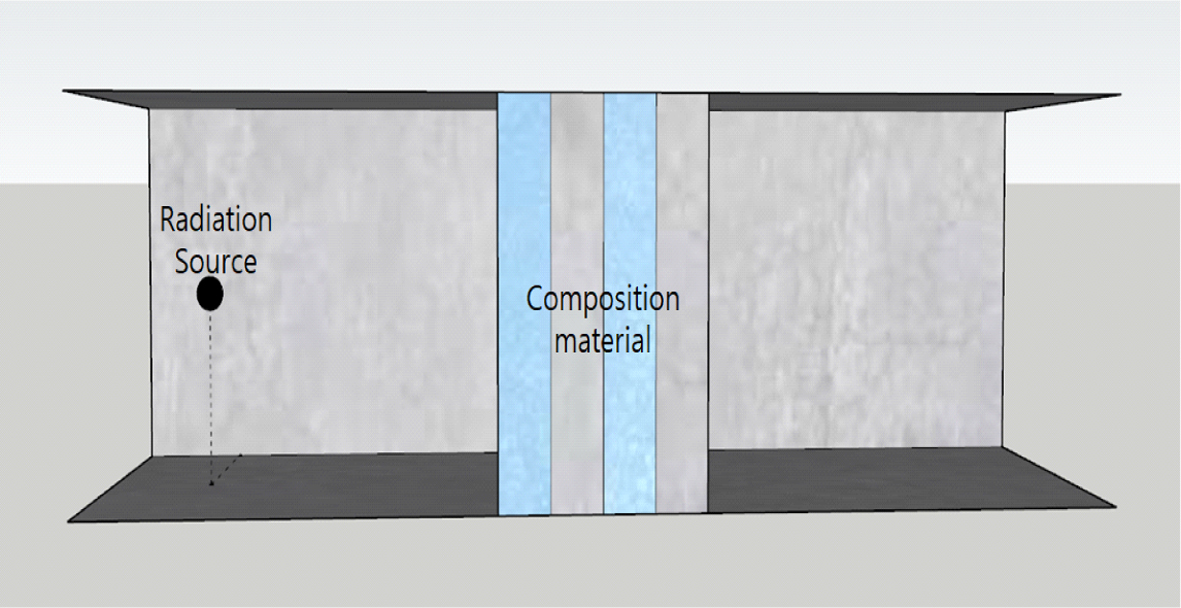
Geometry. 시뮬레이션 상의 구조는 Figure 2와 같다. 사방이 두꺼운 콘크리트로 막힌 30×30×100 cm의 직육면체 공간 안에서 길이방향으로 왼쪽 벽에서 10 cm 떨어진 위치에 방사선원이 존재하며 정 중앙에 복합재를 위치시켰다. 복합재를 통과하기 전과 후의 방사선량을 시뮬레이션으로 얻어내 선감쇠계수를 계산하였다.
재료. 시뮬레이션에 적용한 복합재에는 대표적인 고분자인 폴리에틸렌(PE)과 방사선 차폐재로 알려진 콘크리트, 납, 구리, 텅스텐을 사용하였다. PE/콘크리트, PE/납, PE/구리, PE/ 텅스텐의 각각의 복합재에 1, 10, 30, 50, 80, 100 MeV로 저에너지 영역에서 에너지를 달리한 감마선을 조사해가며 감마선의 에너지의 크기, 재료의 다양성, 복합재의 구조(계면의 넓이)를 고려하였다.

I₀ = 초기 방사선량
I_t = 두께 t인 차폐재를 통과한 방사선량

µ = 복합재의 선형감쇠계수
t = 차폐재의 두께

식 (2)를 식 (1)에 대입하면 다음과 같은 식을 얻을 수 있다.

복합재 내 재료간 계면에 의한 선형감쇠계수 변화를 무시하면 식 (3)을 이용하여 두 재료로 이루어진 복합재의 선형감쇠계수를 구할 수 있다.
재료 A와 재료 B로 이루어진 층상 복합재에 의해 차폐된 선량은 A에 의해 차폐된 선량과 B에 의해 차폐된 선량의 합과 같다. 복합재에 조사된 방사선은 A를 통과 후 B를 통과하므로 B를 통과하는 초기 방사선량은 A를 통과한 방사선량과 같다.
따라서 식 (3)에 의해 복합재에 의해 차폐된 방사선량은 다음과 같이 계산된다.

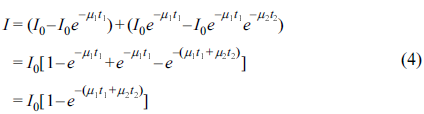
µ₁ = A의 선형감쇠계수
µ₂ = B의 선형감쇠계수
t₁ = A의 두께
t₂ =B의 두께 (t = t₁ + t₂)

식 (3)과 식 (4)에 의해 복합재의 선형감쇠계수는 식 (5)와 같이 계산될 수 있다.

µ_cal = 복합재의 선형감쇠계수 계산값

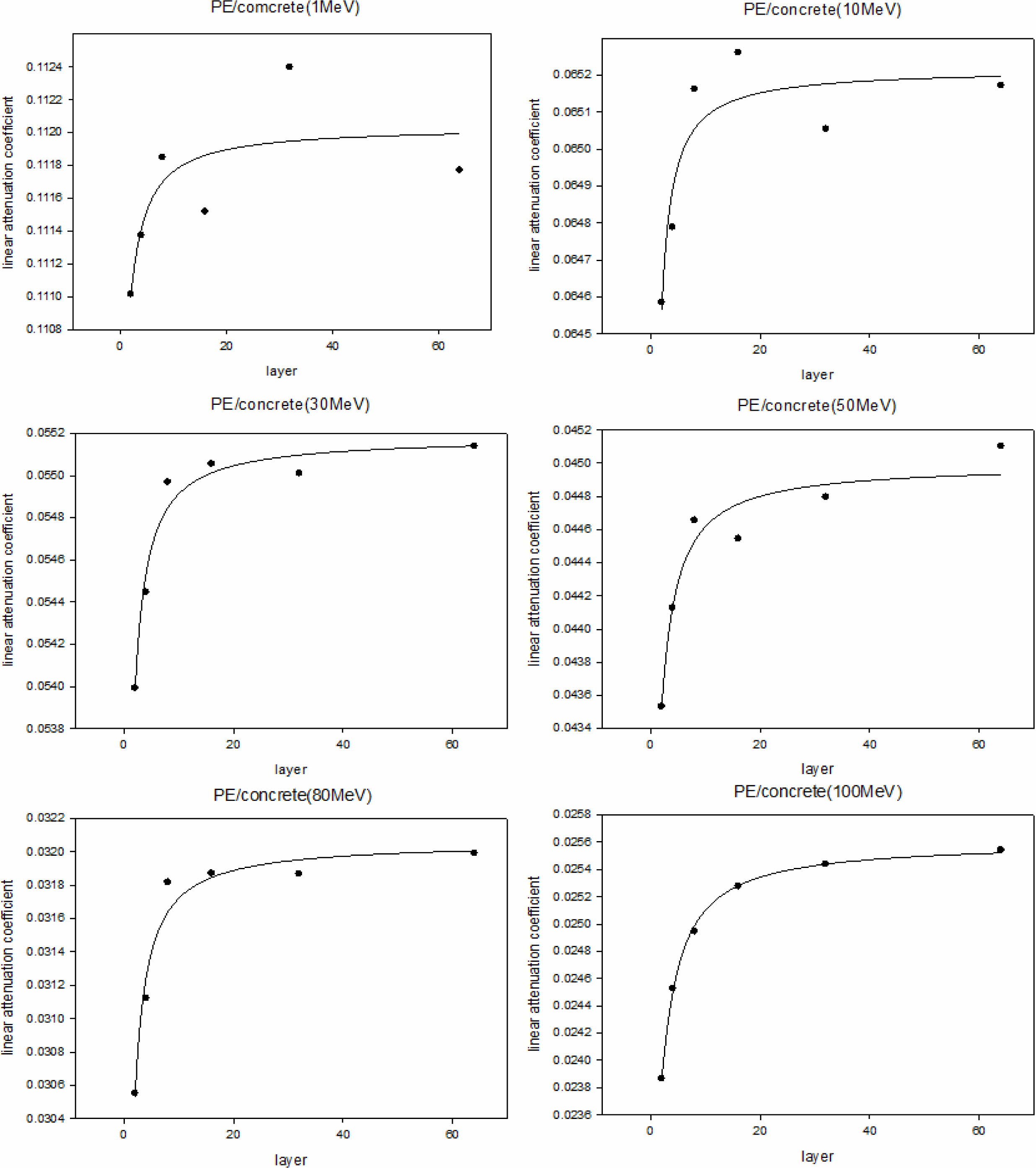
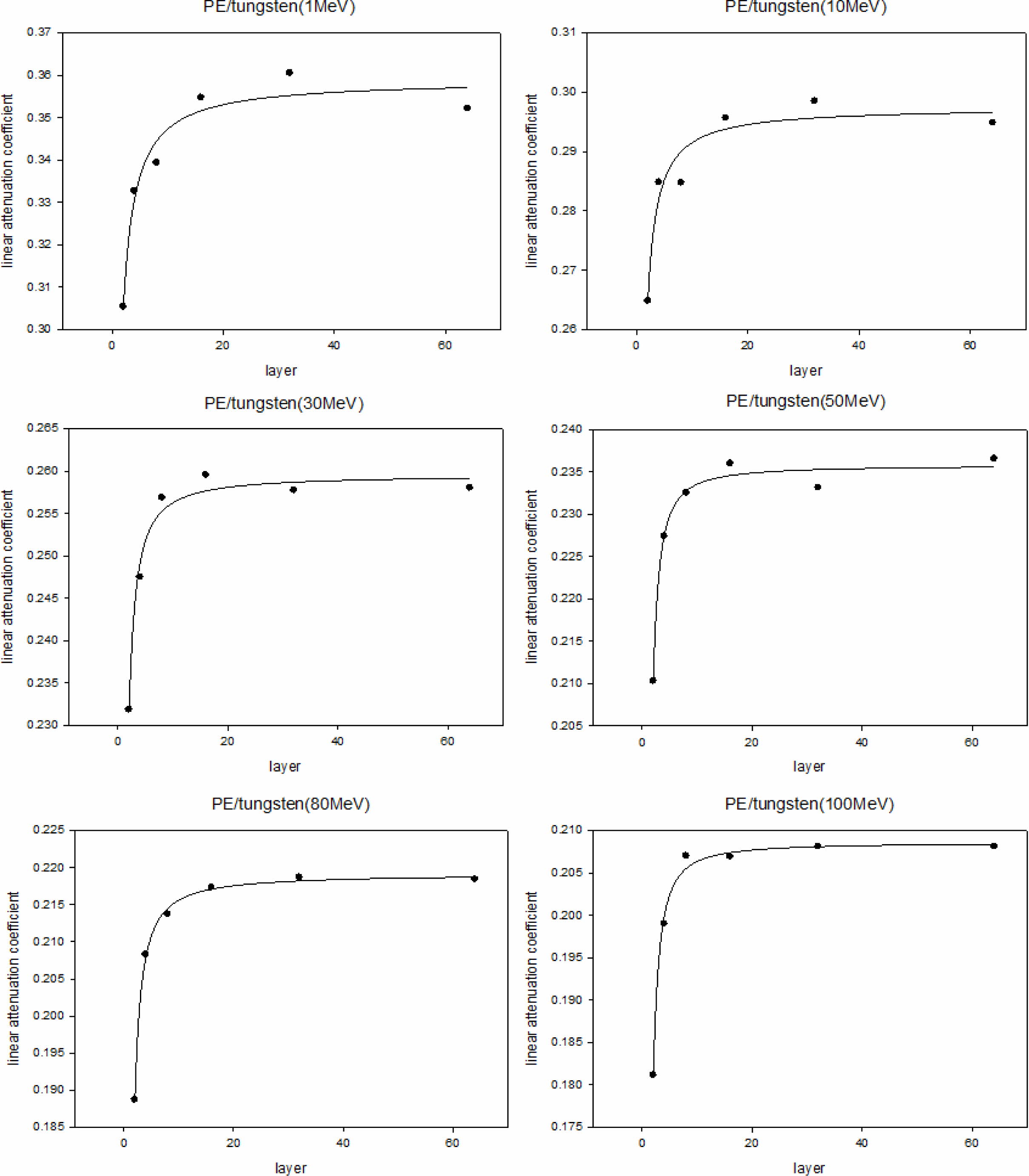
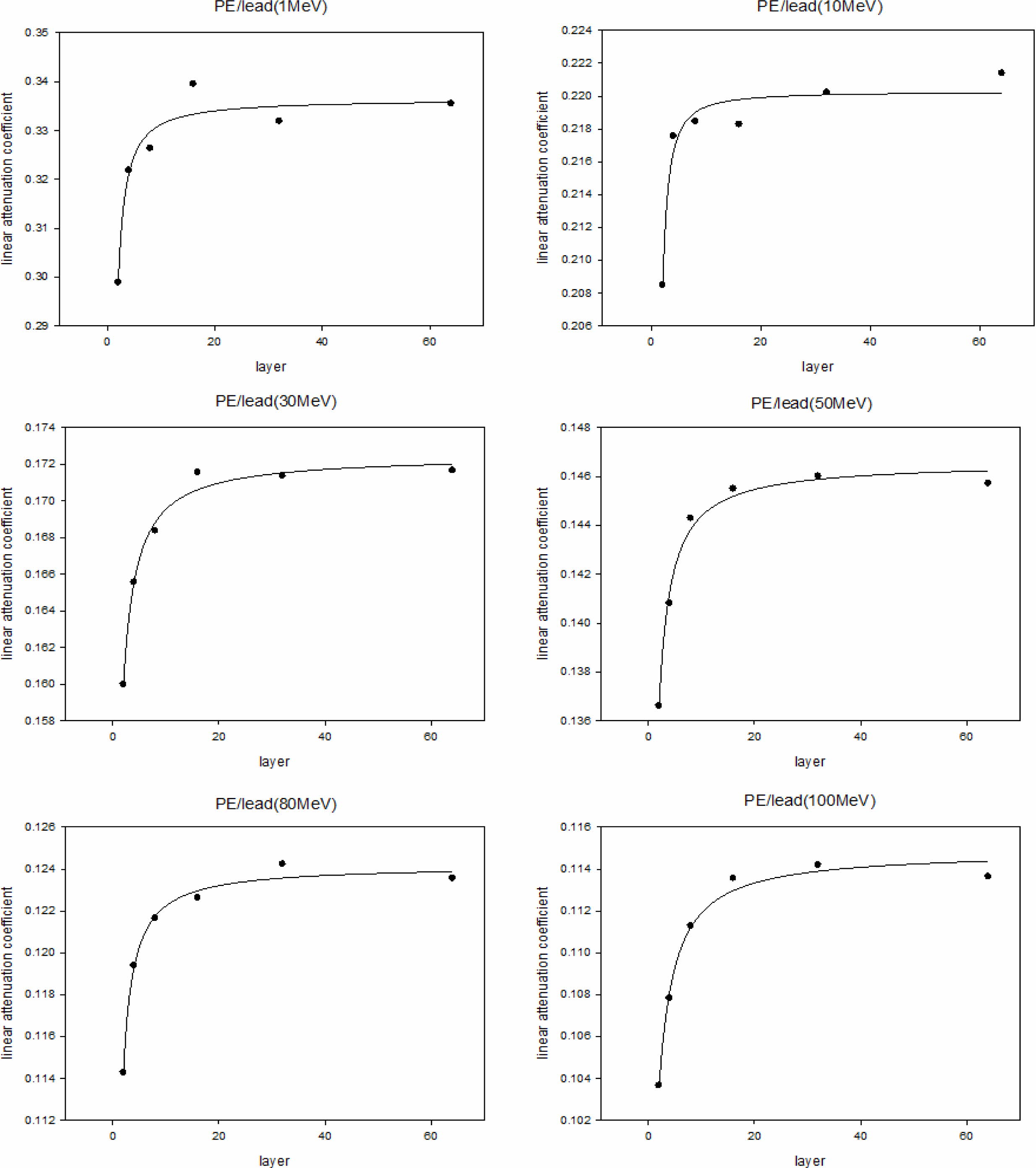
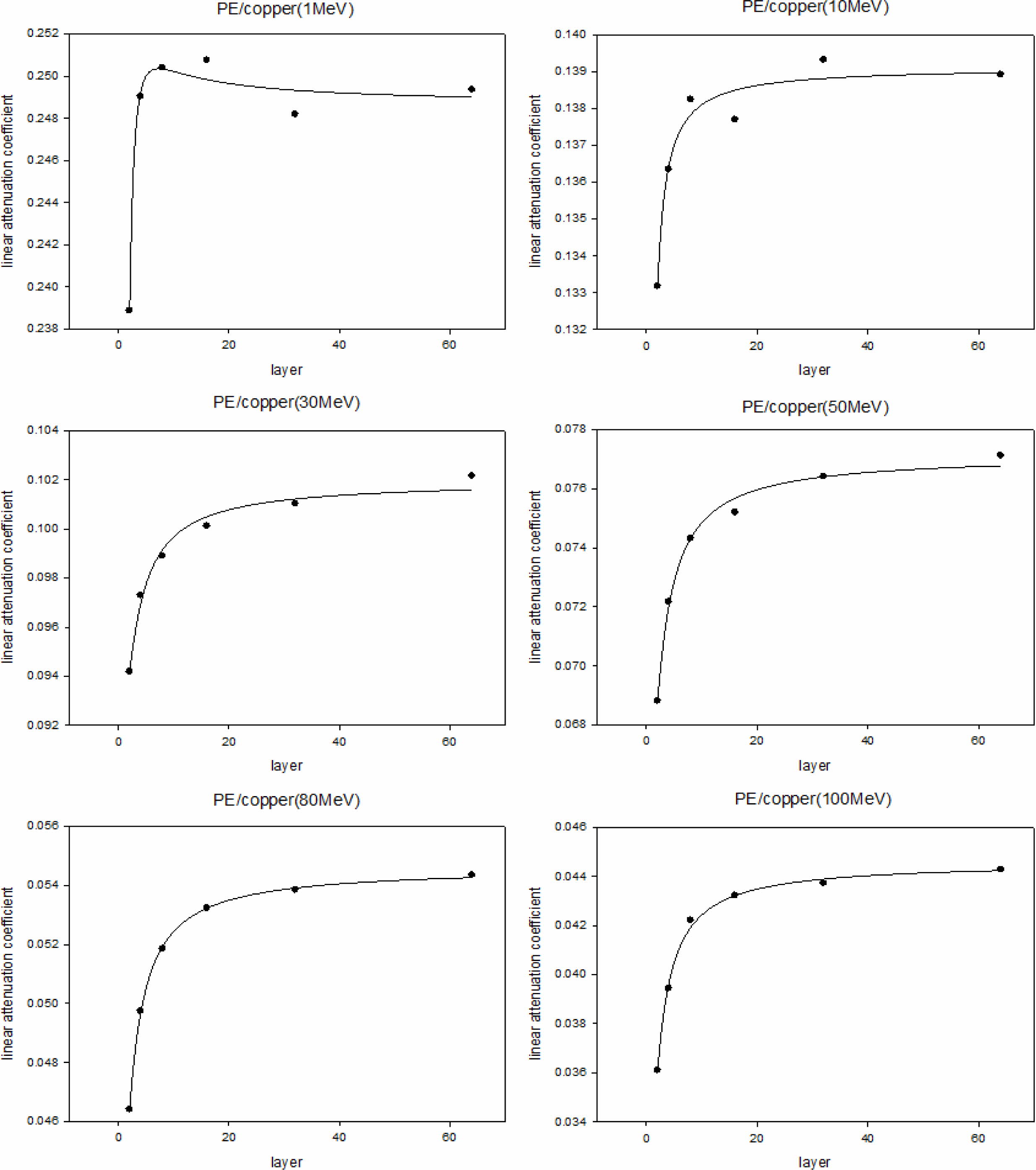
시뮬레이션을 통해 계산된 선형감쇠계수. Figures3-6은 각각 PE/콘크리트, PE/납, PE/구리, PE/텅스텐 복합재의 시뮬레이션 결과를 나타내며 시뮬레이션을 통해 얻어진 선형감쇠계수와 식 (5)를 통해 계산된 선형감쇠계수를 제시하였다. 또한 각각의 그래프는 감마선의 에너지 레벨에 따라 layer 수와 선형감쇠계수 값의 관계를 나타내며 그 관계를 설명할 수 있는 함수를 추론하여 제시하였다. Figures3-6에 표기된 layer 개수는 본 시뮬레이션 상에서 설정한 임의의 값으로 모든 경우에 적용되는 정량적 인자로 보기에는 어려움이 있다. 따라서 layer 개수를 복합재 내 계면의 넓이로 적용시키고 정량적인 해석 대신 그 경향만으로 시뮬레이션 결과를 분석하였다. 이에 따라 layer 개수 항이 포함되지 않은 상수에 대해서만 정량적 분석만 가능했다.
선형감쇠계수의 크기는 PE/텅스텐(Figure 6), PE/납(Figure 4), PE/구리(Figure 5), PE/콘크리트(Figure 3) 순이었으며 이는 각 재료의 선형감쇠계수나 밀도를 고려했을 때 예측할 수 있는 결과였다. 또한 감마선의 에너지의 크기가 증가할수록 선형감쇠계수는 작아졌으며 에너지가 큰 감마선일수록 차폐가 어려워진다는 사실에서 당연한 결과라고 생각할 수 있었다.
시뮬레이션을 통해 계산된 선형감쇠계수와 계면 넓이와의 관계는 감마선의 에너지 크기에 상관없이 모든 재료에서 같은 경향을 보였다(Figure 3-6). 복합재의 선형감쇠계수는 두 재료간 계면이 넓어짐에 따라 증가하는 형태를 보였으며, 계면의 넓이의 차이로 인해 나타나는 선형감쇠계수 값의 차이는 PE/콘크리트 약 0.0012 (cm^-1), PE/납 약 0.011 (cm^-1), PE/구리 약 0.008 (cm^-1), PE/텅스텐 약 0.029 (cm^-1)로 두 물질의 감쇠계수 차이가 클수록, 밀도차가 클수록 크게 나타났다. 즉, 감마선 차폐능은 복합재에 사용된 두 물질의 감쇠계수 차이가 클수록 재료간 계면 넓이의 영향을 많이 받는다는 것을 알 수 있었다.
선형감쇠계수와 계면 넓이의 관계식은 재료의 종류와 감마선의 에너지 크기에 관계없이 아래 함수로 나타낼 수 있었다.

x = layer 수

각 재료 및 에너지에 따라 식 (6)의 형태로 얻어진 함수의 상수(µ₀, a, b)값은 Figures3-6에 제시하였으며 앞서 계산한 µ_cal 값과의 비교를 위해 함께 표기하였다. Figures 3-6에 제시된 R_sqr(R-squared) 값은 결정계수 값으로 데이터 표본을 통해 추정한 회귀선이 어느 정도 적합한 것인가를 설명해주는 계수이다. 결정계수는 0과 1사이 값을 가지며 이 값이 1에 가까워질수록 표본데이터가 추정된 회귀선으로 완전한 설명이 가능하다는 것을 의미한다.
시뮬레이션에 적용한 구조가 두꺼운 콘크리트 상자 내에 존재하므로 콘크리트 벽에 산란 및 반사된 방사선에 의해 일부 오류가 발생할 것으로 생각했음에도 불구하고 대부분의 결정계수가 0.9를 넘는 값을 나타내는 것으로 시뮬레이션의 결과 값이 비교적 식 (6)을 잘 따르는 것으로 판단할 수 있다.
이 때, µ₀에는 계면 넓이에 대한 항이 포함되어 있지 않으므로 이 항은 복합재의 구조, 즉 계면의 넓이에 상관없이 재료에 의해 결정되는 항으로 볼 수 있다. 실제로 앞서 유도한 선형감쇠계수 식을 이용하여 계산한 계산 값과 µ₀를 비교해보면 그 차이가 크지 않음을 알 수 있다.
감마선은 에너지가 큰 전자기파이므로 투과력은 높지만 이론적으로 전자기파에 속하기 때문에 특성이 다른 매질에 입사했을 때 일부 굴절이 일어나게 된다. 따라서 복합재를 차폐재로 이용했을 경우 재료에 의한 감쇠효과가 크겠지만 복합재 구조에 의한, 즉, 감마선이 통과하는 매질이 달라지는 계면에서의 감쇠도 발생한다. 이에 대한 인자를 앞서 도출한 함수에 추가하기 위해 식 (5)에 의해 계산된 선형감쇠계수와 시뮬레이션 결과로 얻어진 µ₀값의 차이(µ₀-µ_cal)를 분석하였다.
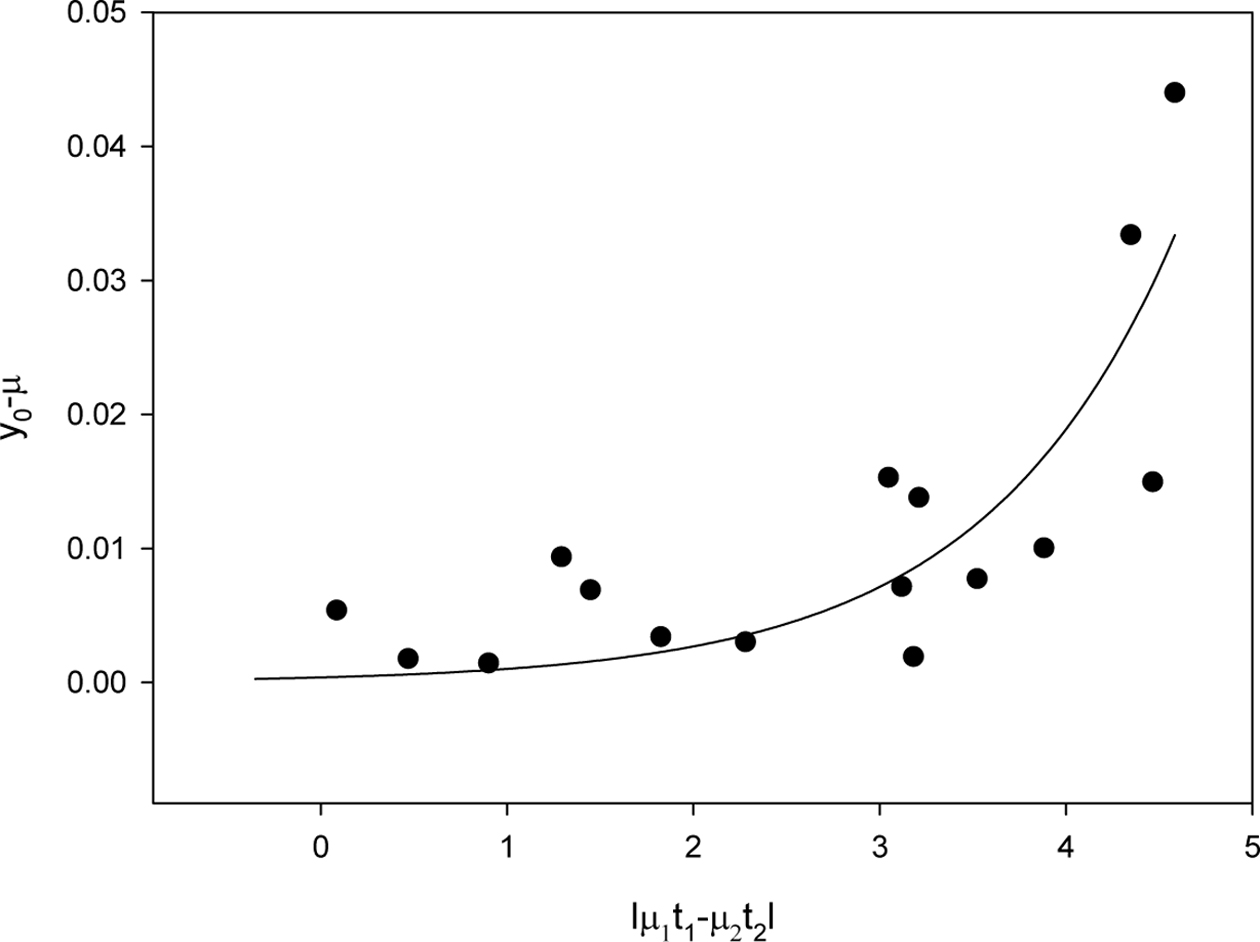
µ₀-µ_cal 값은 복합재에 사용된 두 물질의 감쇠계수 차이가 커질수록 커지는 경향을 보였으며, 이를 Figure 7에 나타냈다. 이 때, 두 재료의 계면을 통과하면서 감마선이 강해지는 경우는 없으므로 µ₀-µ_cal 값이 0보다 작은 음수가 되는 경우는 제외했다.
위 그래프를 통해 선형감쇠계수의 계산 값과 µ0의 차이 값은 다음 식과 같은 관계를 가지고 있음을 도출할 수 있었다.

따라서 식(6)의 µ0는 식 (5)와 식 (7)에 의해,

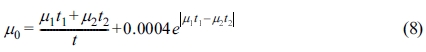
로 정의할 수 있다.
이 외에 식 (6)의 a의 값은 대체로 음수로 나타나며 a/x의 형태에 의해 계면의 넓이가 증가할수록 전체 값은 µ₀에 가까워지는 것을 알 수 있다. 이를 통해 계면의 개수가 최대로 증가했을 때, 즉, 두 재료간 계면의 면적이 매우 넓은 복합재의 선형감쇠계수는 µ₀와 같다고 할 수 있으며 복합재의 선형감쇠계수 최댓값은 µ₀인 것으로 판단할 수 있다.
한편, 식 (6)의 a와 b에 대한 분석도 필요하나 식에 x 값으로 포함된 layer의 수는 본 시뮬레이션에만 적용되는 값일 뿐 절대적인 계면단면적이 될 수 없으므로 x와 관계된 두 값은 진행된 시뮬레이션만으로는 도출해내기에 무리가 있다고 생각되어 a와 b로 남겨두었다. a, b에 대한 정의는 할 수 없었으나 두 값이 크지 않아 이후 진행된 검증단계에서는 두 값을 무시하고 µ₀ 값만을 이용했다. 본 연구에서 진행된 시뮬레이션에서는 이성분 복합재만을 대상으로 하였으며 복잡한 구조의 복합재의 경우 이를 도식화 하는데 어려움이 있어 시뮬레이션에 적용하지 못했다. 예를 들어, 다공성 물질을 이용해 물질간 계면을 넓혀 감마선의 산란을 야기시키거나, 섬유 또는 입자형태의 첨가물이 포함된 복합재의 경우는 본 연구에서 도출된 식으로 설계하기에는 한계가 있다. 따라서 이와 같은 복합재의 구조의 영향에 대한 연구가 추가적으로 진행되어 이를 해석할 수 있는 항이 포함될 수 있도록 한다면 보다 신뢰성 있는 식이 도출될 수 있을 것으로 생각된다.
도출된 식의 적용. 시뮬레이션을 이용해 도출된 식 (8)이 실제 다양한 상황에서 적용 가능한지 알아보기 위해 이미 발표된 차폐실험 논문들의 데이터와 식 (8)을 적용한 계산 값을 비교하였다.
H. E. Hassan의⁹ 연구를 통해 콘크리트와 콘크리트/산화납 복합재의 강도 662 keV의 감마선에 대한 질량 감쇠계수를 알 수 있었다. 위에서 도출된 식은 선형감쇠계수에 대한 식이므로 밀도를 곱해 선형감쇠계수 값을 구할 수 있으며 산화납의 선형감쇠계수는 H. O. Tekin의¹⁰ 연구결과를 통해 알 수 있었다. 복합재에 사용된 산화납의 질량분율을 부피분율로 변환하고 각 값을 식 (8)에 대입하면 선형감쇠계수의 계산 값을 구할 수 있다. H. E. Hassan의⁹ 연구논문에 따르면 콘크리트에 10 wt%의 산화납이 첨가된 복합재의 경우, 강도 662 keV의 감마선에 대해 0.145 cm^-1의 선형감쇠계수 값을 가지며, 식 (8)을 통해 계산된 선형감쇠계수는 0.158 cm^-1가 된다.
Le Chang의11 연구에서는 에폭시레진에 텅스텐 미세입자가 첨가된 복합재의 코발트에서 방사되는 감마선에 대한 질량 감쇠계수를 알 수 있다. Le Chang의¹¹ 연구에서 발표한 데이터에 따르면 에폭시레진에 텅스턴 입자가 30 wt% 첨가된 복합재의 선형감쇠계수는 0.104 cm^-1이며, 위와 같은 방법으로 식 (8)에 각 값을 대입하면 선형감쇠계수의 계산 값 0.106 cm^-1을 얻을 수 있다. 이 때 텅스텐의 선형감쇠계수는 D. R. McAlister의¹² 연구논문을 통해 얻어진 값을 사용하였다.(µ0-µcal

본 연구에서는 MCNP(Monte Carlo n-patricle transport code) 시뮬레이션을 통해 다양한 재료 및 조건에 대한 차폐율을 계산해보고 이를 이용해 모든 재료에 적용해 차폐능을 계산할 수 있는 차폐 식을 도출하고자 하였다.
복합재의 구조를 생각하지 않은 선형감쇠계수항은 많이 알려진 식으로 쉽게 구할 수 있었으며 보다 실제와 비슷하게 계산하기 위해 시뮬레이션을 이용하였다. 시뮬레이션을 통해 계산된 선형감쇠계수는 에너지 크기에 상관없이 모든 재료에서 같은 경향을 보였다. 이 경향으로 복합재의 선형감쇠계수를 계산할 수 있는 식을 도출해낼 수 있었다. µ₀는 다음과 같이 계산될 수 있으며 이 값은 두 재료로 이루어진 복합재가 가질 수 있는 선형감쇠계수의 최댓값으로 생각된다.

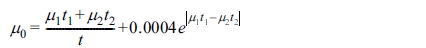
다음과 같이 계산될 수 있으며 이 값은 두 재료로 이루어진 복합재가 가질 수 있는 선형감쇠계수의 최댓값으로 생각된다. 앞으로 검증 및 보완의 단계가 더 필요하겠지만 위 식을 통해 보다 효율적으로 복합재로 이루어진 차폐재의 설계가 가능할 수 있을 것으로 기대된다.